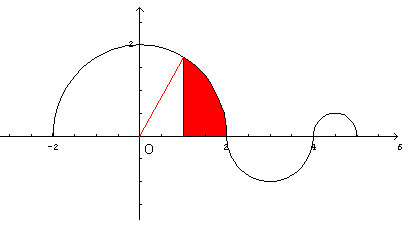
Per x compreso tra -2 e +2 il diagramma è quello di una semicirconferenza con centro in O
e raggio 2. Da ![]() si ottiene
si ottiene
![]()
Per x compreso tra +2 e +4 il diagramma è quello di una semicirconferenza con centro in (3;0)
e raggio 1. Da ![]() si ottiene
si ottiene
![]()
Per x compreso tra +4 e +5 il diagramma è quello di una semicirconferenza con centro in (9/2;0)
e raggio 1/2. Da ![]() si ottiene
si ottiene
![]()
Il grafico proposto evidenzia che la funzione non è derivabile per x=-2, x=2, x=4 e x=5 in quanto per questi valori della variabile la tangente alla curva risulta priva di coefficiente angolare. In particolare per x=2 e x=4 ci sono flessi verticali.
Condizione necessaria perché la funzione continua f ammetta punti stazionari negli intervalli in cui è derivabile è che si annulli la derivata prima, cioè g. Ciò si verifica per x=2 e x=4. A sinistra di 2 g=f' è positiva mentre a destra di 2 è negativa. Per x=2 f ha un massimo relativo; per ragioni analoghe per x=4 f ha un minimo relativo.
Il valore della funzione integrale proposta è espresso graficamente dall'area sottesa dal grafico di g a partire dall'estremo inferiore -2.
Per avere f(4) basta sottrarre l'area della seconda semicirconferenza da quella della prima. Si ha
![]()
Per avere f(1) si può sottrarre dall'area della prima semicirconferenza l'area del mezzo segmento circolare sotteso dall'arco con estremi di ascissa 1 e 2. A sua volta quest'ultima area si può ottenere sottraendo dall'area del settore circolare di ampiezza 30° l'area del triangolo rettangolo di cateti 1 e √3.
Si ottiene
![]()
La derivata seconda di f coincide con la derivata prima di g e si annulla nei punti stazionari di g. Quindi è nulla per x=0, x=3 e x=9/2.
Il segno di f è 0 per x=-2 e positivo nel resto del dominio poiché per x>-2 l'integrale di g risulta positivo.
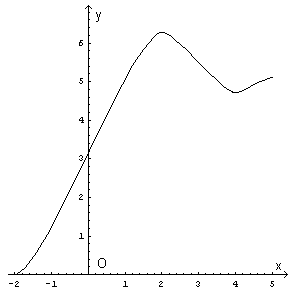
Riunendo tutte le proprietà di f dedotte nelle analisi precedenti il suo diagramma mostra il seguente andamento