, si può ottenere una sequenza finita di numeri naturali
nel seguente modo(note a cura di Roberto Bigoni)
Un numero razionale, per definizione, è rappresentabile con una frazione cioè con il rapporto tra due numeri interi. Infatti il termine razionale deriva dal termine latino ratio che significa rapporto.
Da ogni frazione positiva ridotta ai minimi termini
, si può ottenere una sequenza finita di numeri naturali
nel seguente modo
dove a0 è il massimo numero naturale ≤ ,
cioè la parte intera del quoziente
di n diviso d, r0 il resto intero di questa divisione e d0 coincide
con il denominatore d.
Ad esempio: 
. Il questo caso
a0=2 e r0=3.
Se r0 è uguale a 0, cioè se il numeratore è un multiplo del denominatore, la procedura termina. Altrimenti dalla (1) si ha
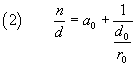
Ovviamente d0 è maggiore di r0 e la frazione
può essere trattata come la frazione , cioè
dove a1 è il quoziente intero di d0 diviso r0 e r1 il resto di questa divisione. Dalle (2) e (3) si ottiene
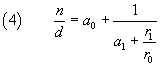
Nell'esempio proposto si ha
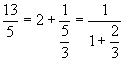
Ancora, se r1 è uguale a 0, la procedura termina. Altrimenti dalla (4) si ha
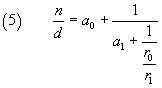
A sua volta 
può essere scritta come
dove a2 è il quoziente intero di r0 diviso r1 e r2 il resto di questa divisione.
Dalle (5) e (6) si ottiene
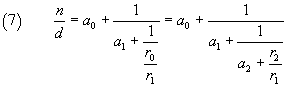
Nell'esempio proposto si ha
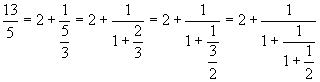
Nell'esempio si vede che r2, l'ultimo resto ottenuto, è uguale a 1. Quando si ottiene un resto 1, è ovvio che nel passo successivo si otterrà resto 0, quindi si può terminare la procedura assumendo come ultimo valore an della sequenza il resto precedente. Nell'esempio si ha a3=2. Fintanto che non si ottiene resto 1 la procedura va reiterata.
Nell'esempio proposto si è visto che dalla frazione
si ottiene la sequenza
[2;1,1,2]. Questa sequenza è detta sviluppo in frazione continua della frazione
.
Gli elementi dello sviluppo in frazione continua si possono ottenere velocemente dall' algoritmo di Euclide per il calcolo del Massimo Comun Divisore tra due numeri naturali, registrando ad ogni passo i successivi quozienti ottenuti fino a che non si ottiene resto 0.
Esempio:
| 13 | 5 | 3 | 2 | 1 |
| quoziente | 2 | 1 | 1 | 2 |
| resto | 3 | 2 | 1 | 0 |
Un esempio un po' più complicato: 
| 157 | 2791 | 157 | 122 | 35 | 17 | 1 |
| quoziente | 0 | 17 | 1 | 3 | 2 | 17 |
| resto | 157 | 122 | 35 | 17 | 1 | 0 |
Lo sviluppo in frazione continua di è
quindi [0; 17, 1, 3, 2, 17].
Questo secondo esempio evidenzia una interessante proprietà: nello sviluppo di una frazione minore di 1 il primo termine è 0 e i termini seguenti coincidono con quelli della sua reciproca.
Da uno sviluppo in frazione continua è possibile ottenere la frazione generatrice invertendo la procedura precedentemente esposta: partendo dall'ultimo termine dello sviluppo, se ne calcola il reciproco e lo si aggiunge al termine precedente; si calcola il reciproco di questa somma e lo si aggiunge fino ad arrivare al primo termine. Riprendendo il primo degli esempi proposti si ha:
Per il secondo esempio si ha:
Può risultare utile la seguente applicazione Javascript. Il bottone A Continua sviluppa un numero razionale, espresso come frazione o come decimale, in frazione continua;
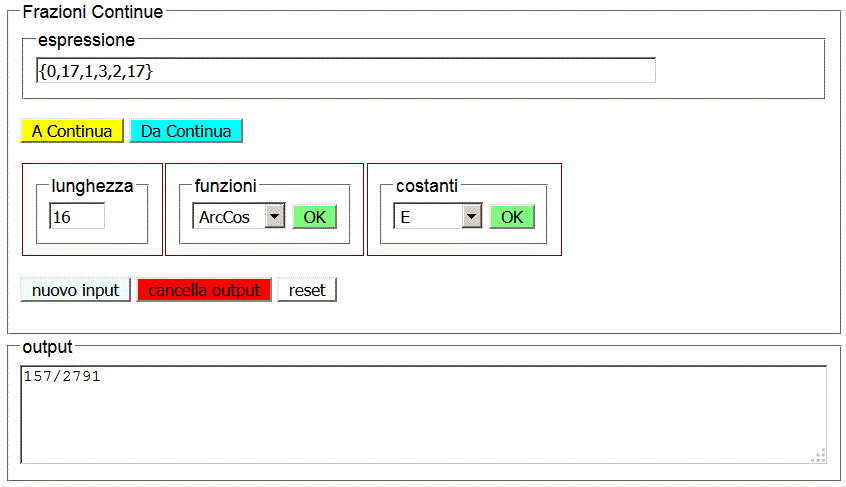
il bottone Da Continua compie l'operazione inversa.
Il campo lunghezza permette di fissare il massimo numero di elementi dello sviluppo.
Esempi.
A Continua
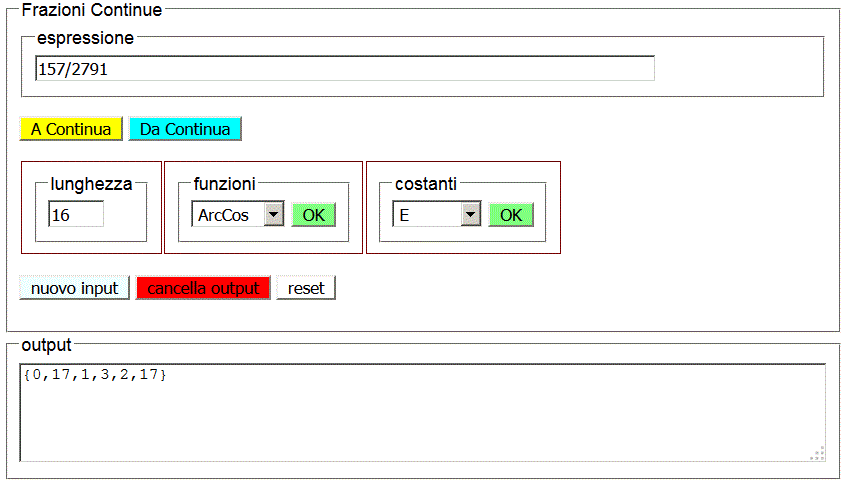
Da Continua
Un numero irrazionale, per definizione, non può essere rappresentato dal rapporto fra due numeri interi, quindi ad un numero irrazionale non si può applicare l'algoritmo di Euclide per ottenerne lo sviluppo in frazione continua finita per lo stesso motivo per cui non è possibile ottenerne una rappresentazione finita qualunque sia la base adottata. È noto che la rappresentazione decimale di un numero irrazionale è un decimale aperiodico, ma si otterrebbero binari aperiodici se si volesse rappresentarlo in base due o esadecimali aperiodici se lo si volesse rappresentare in base sedici. Tuttavia, almeno in alcuni casi è abbastanza semplice, con un procedimento analogo a quello usato per i numeri razionali, dedurne uno sviluppo in frazione continua infinita.
Si consideri, ad esempio, la radice quadrata di due, che è stato uno dei primi irrazionali scoperti nella storia della matematica occidentale nell'ambito della scuola pitagorica. Si ha
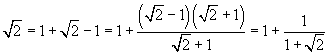
In definitiva
Applicando ricorsivamente questa identità alle radici di due nei denominatori si ottiene
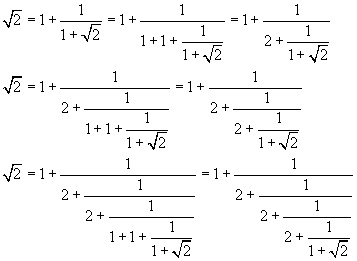
Ovviamente questa procedura ricorsiva può essere sempre ripetuta, quindi la procedura non ha fine, ma non è azzardato affermare che lo sviluppo in frazione continua della radice di due è
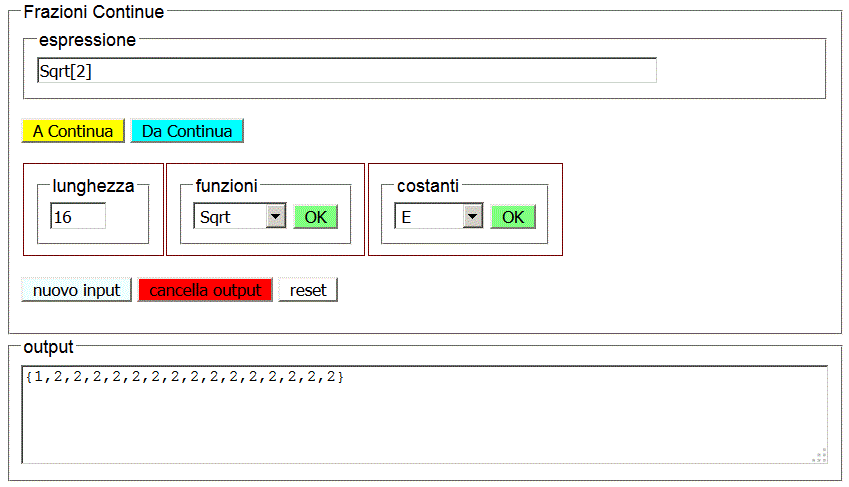
La radice quadrata di 2, che rappresentata in base dieci è un decimale aperiodico, sviluppata in frazione continua ha uno sviluppo infinito ma evidentemente periodico con antiperiodo 1 e periodo 2.
Un altro esempio piuttosto interessante è offerto dal numero aureo Φ. Si ha
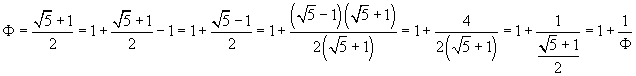
In definitiva
Applicando ricorsivamente questa identità ai numeri Φ nei denominatori si ha
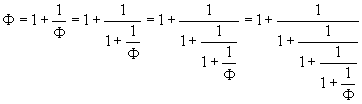
Lo sviluppo in frazione continua di Φ è quindi
In generale, per ogni numero reale x si ha
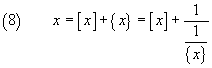
dove [x] rappresenta il massimo intero ≤ x, cioè la sua parte intera,
e {x} = x-[x], cioè la sua parte frazionaria.
Il reciproco 
della parte frazionaria,
se questa non è nulla, è un numero reale maggiore di 1 che a sua volta può essere espresso come somma tra la sua
parte intera e la sua parte frazionaria.
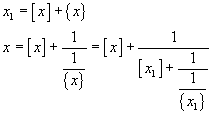
Ora si indica con x2 il reciproco della parte frazionaria di x1 e si continua come sopra in un processo che non ha mai fine, ottenendo la sequenza costituita dalle parti intere dei numeri xi successivamente trovati, quindi lo sviluppo in frazione continua di x risulta
Volendo usare la calcolatrice del paragrafo 2 per ottenere lo sviluppo in frazione continua della radice quadrata di 2 non ha senso scrivere in input una
approssimazione decimale della stessa, ad esempio 1.41421356, perché si otterrebbe lo sviluppo di un numero razionale che risulterebbe finito.
Si possono, in questo caso come in altri analoghi,
usare le funzioni del selettore funzioni che riporta in input uno dei nomi delle funzioni di variabile realepiù usate.
Si possono inoltre usare, dal selettore costanti, alcune delle costanti reali più note come π, e, Φ.
Esempi.
√2
Φ
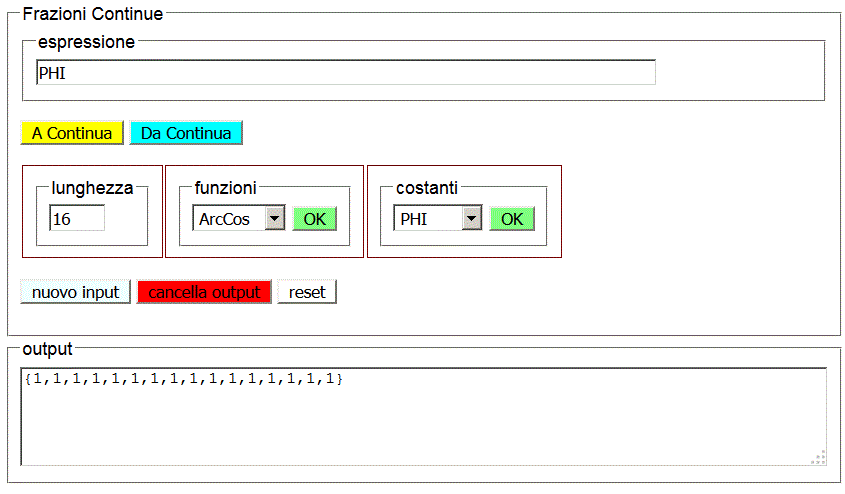
Da Continua su uno sviluppo inevitabilmente limitato di Φ produce una approssimazione razionale a Φ.
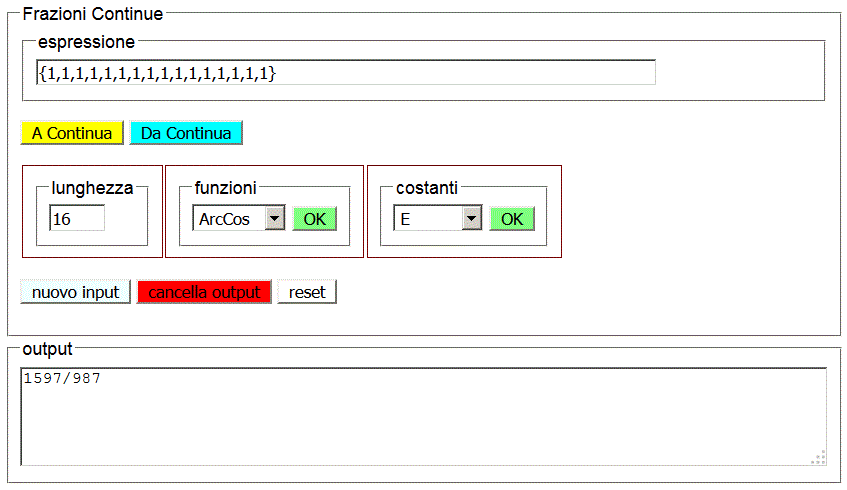
Risultati analoghi si possono ottenere da Mathematica, se si è installato questo software, o gratuitamente da WolframAlpha (documentazione) che fornisce in rete alcune funzionalità di Mathematica.
In generale, lo sviluppo di un numero irrazionale in frazione continua è un buon modo di ottenere una sua approssimazione razionale:
il numero Φ che può essere approssimato, ad esempio, dal rapporto tra un numero della
successione di Fibonacci e il precedente, con approssimazioni
tanto migliori quanto più si sale nella successione di Fibonacci, può anche essere approssimato a piacere dal suo sviluppo in
frazione continua, costituito da una sequenza infinita di 1. Si può anche assumere questo fatto per definire Φ: è il numero
rappresentato da 
dove sopralineatura del secondo 1
indica la sua periodicità.
Lo stesso vale per 
.
In generale le radici quadrate di numeri naturali hanno sviluppi periodici.
Questo è abbastanza semplice da dimostrare se il radicando è il successivo di un quadrato; si ha infatti
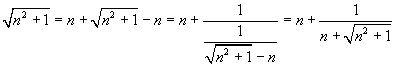
quindi
Applicando ricorsivamente la (10) si ha
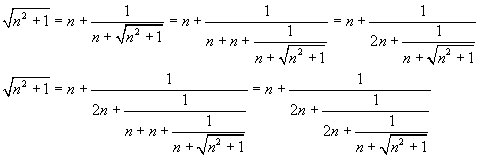
In definitiva
Dalla (11)
Se il radicando supera di 2 i quadrato di un numero naturale si ha
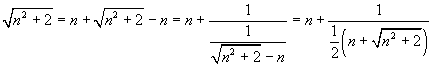
quindi
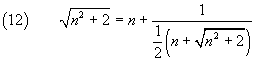
Applicando ricorsivamente questa identità si ottiene
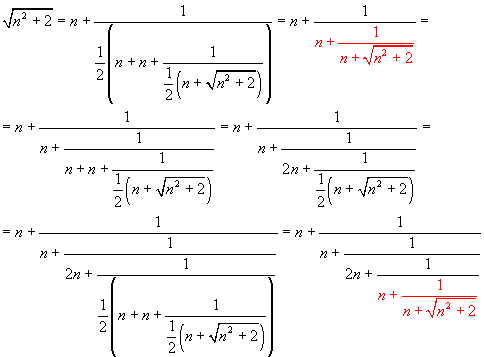
L'ultimo denominatore ottenuto coincide con quello della prima riga: il ciclo si ripete regolarmente, quindi
Dalla (13)
Viceversa una frazione continua periodica può essere espressa dalla soluzione di un'equazione di secondo grado
con coefficienti naturali.
Esempio: frazione con periodo di 2 cifre
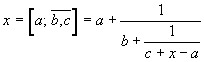
Il numero x si ottiene dalla soluzione positiva dell'equazione
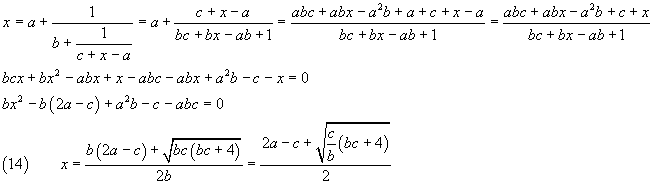
Casi particolarmente semplici si hanno dalla (14) per con c=2a e multiplo di b. Esempi:
Dalla (9), per x=cotanh(1), usando una calcolatrice, si ha
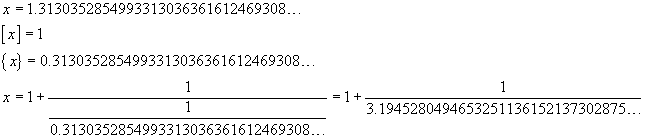
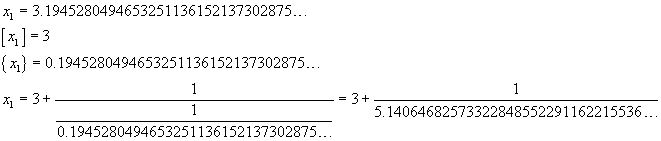
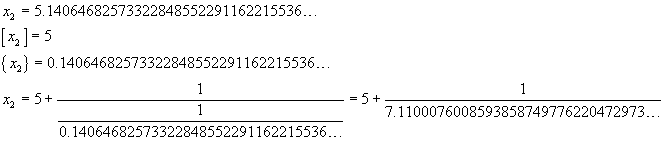
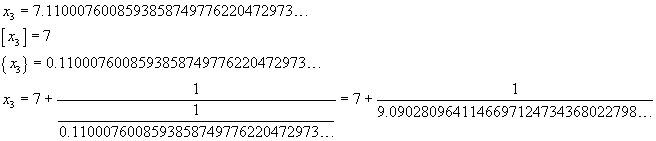
Usando la calcolatrice del paragrafo 2, si ottiene
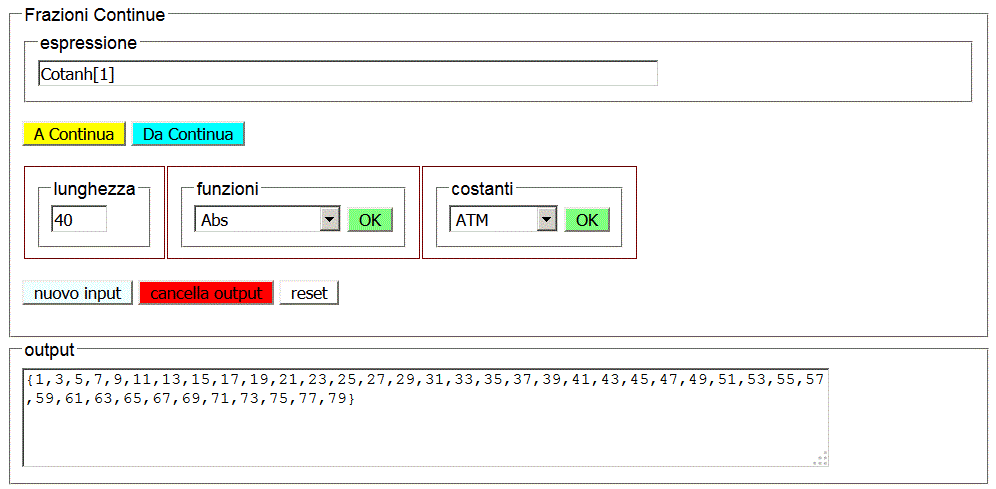
Ovviamente lo sviluppo in frazione continua di cotanh(1) non è periodico, ma mostra una notevole regolarità: si può congetturare che sia dato dalla sequenza dei numeri dispari.
In effetti la congettura è giusta ed è stata dimostrata da Eulero.
Per la base dell'esponenziale naturale, cioè il numero di Eulero e, si ottiene
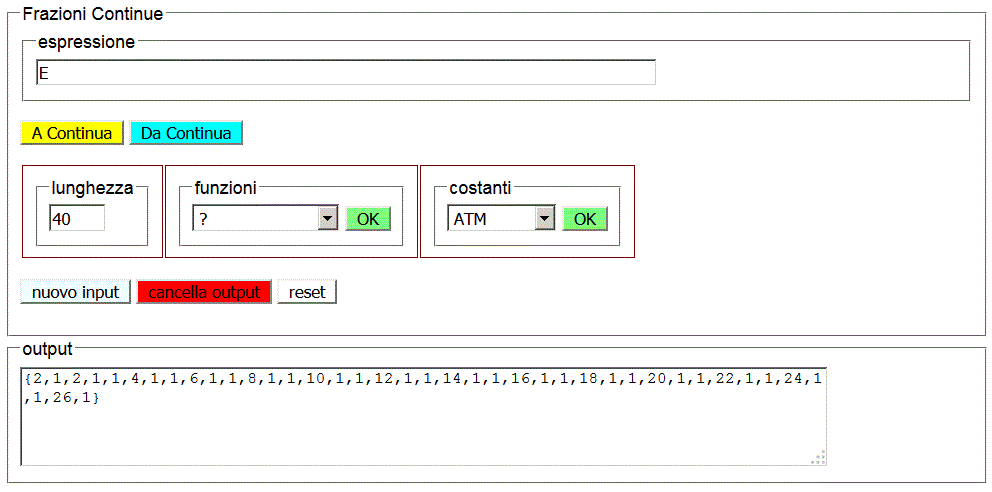
Anche in questo caso si nota una evidente regolarità: a partire dal terzo termine si hanno i numeri pari seguiti da una coppia di 1. Si può congetturare che lo sviluppo in frazione continua di e sia
Prolungando opportunamente questa sequenza e calcolandone la frazione generatrice, si può approssimare e con la precisione desiderata.Questo metodo di approssimazione può essere una valida alternativa allo sviluppo in serie di Maclaurin.
ultima revisione Maggio 2018