(note a cura di Roberto Bigoni)
Come è noto dai primi studi aritmetici, i numeri primi sono i numeri naturali maggiori di 1 non risultanti dal prodotto di due numeri minori.
Questa definizione implica che 1 non è primo e che l'unico primo pari è 2.
I numeri primi sono infiniti, cioè non esiste il massimo numero primo. Una dimostrazione per assurdo di questo teorema si deve a Euclide.
Se i numeri primi non fossero infiniti, esisterebbe il massimo numero primo M e sarebbe possibile calcolare il numero P = 2·3·5·7·11·13·…·M, uguale al prodotto di tutti i numeri primi
Si consideri il numero naturale S immediatamente successivo a P: S=P+1.
È impossibile che S sia primo, perché maggiore del massimo primo M.
Dividendo S per qualunque numero primo, si otterrebbe come quoziente il prodotto dei rimanenti numeri primi e resto 1 e quindi S non è divisibile per nessuno dei numeri primi, quindi deve essere primo.
Si ottengono così due affermazioni contraddittorie. Bisogna pertanto ammettere che i numeri primi sono infiniti.
I numeri naturali maggiori di 1 non primi sono detti numeri composti.
Il metodo concettualmente più semplice per ottenere l'insieme Pn dei numeri primi ≤ n (n> 2) è il
crivello di Eratostene
(il crivello o vaglio o setaccio è un attrezzo per filtrare il grano macinato, separando la farina dalla crusca):
Per stabilire se un numero dispari n è primo, cioè per controllarne la
primalità, si può costruire l'insieme Pn e controllare
se n è l'ultimo elemento di Pn.
Se si, n è primo; altrimenti è composto.
La seguente applicazione Javascript calcola i numeri primi ≤ n e l'n-simo numero primo.
Ovviamente, perché essa funzioni a dovere il vostro browser deve abilitare Javascript.
Se il vostro browser non permette i frames interni, potete accedere direttamente alla pagina dell'applicazione.
Se il tempo di calcolo supera i minuti indicati, potete provare ad aumentarli.
Se n è molto grande, il crivello risulta impraticabile per quantità di memoria e tempo di calcolo richiesti. Sono stati quindi cercati e vengono cercati ancor oggi test di primalità diretti, cioè non richiedenti il calcolo di un numero enorme di primi.
Un primo test di primalità si può derivare da un algoritmo di fattorizzazione dovuto a P. de Fermat.
Dato il numero dispari n, il metodo di Fermat si basa sulla ricerca di due numeri h e k tali che
![]()
Se n è un quadrato perfetto, la soluzione è immediata perché il questo caso n è uguale al prodotto della sua radice quadrata per sé stessa e ovviamente n non è primo.
In caso contrario si può sempre esprimere hk come differenza di due quadrati:
![]()
quindi, posto
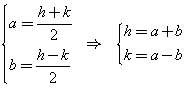
si ha
![]()
Il problema è risolto se si trova un numero a tale a2-n sia un quadrato perfetto.
A questo scopo si procede per tentativi:
Ricavati a e b si ha
![]()
Se a-b = 1, n è primo; altrimenti i due fattori a-b e a+b (cioè h e k) sono diversi e minori di n, quindi il numero è composto.
Il metodo di fattorizzazione di Fermat richiede di controllare ripetutamente se un numero naturale n è un quadrato perfetto.
Non è possibile determinare direttamente questa proprietà di n.
In molti casi è tuttavia possibile escluderla abbastanza velocemente osservando che i residui modulo m, per un numero m prefissato, sono in numero abbastanza ridotto.
Ad esempio, i residui modulo 8 per i quadrati dei primi 100 numeri naturali, utilizzando WolframAlpha, sono

Anche senza una dimostrazione formale, si può tranquillamente congetturare che calcolando il resto della divisione di un numero naturale per 8, se il resto è diverso da 0, 1, 4, il numero non è un quadrato perfetto.
Un ulteriore esempio è fornito dall'insieme dei residui modulo 9.

Anche in questo caso si può tranquillamente congetturare che calcolando il resto della divisione di un numero per 9, se il resto è diverso da 0, 1, 4, 7, il numero non è un quadrato perfetto.
Ma il superamento di test di questo tipo è condizione necessaria ma non sufficiente a stabilire che n è un quadrato perfetto. È quindi utile per diradare il numero dei possibili quadrati perfetti, ma non conclusivo. Una procedura inevitabilmente più dispendiosa che fornisce la sicurezza può essere un algoritmo di bisezione.
Si considera la successione dei numeri naturali qi che, iniziando da 4, è formata da numeri tali che ognuno di essi è il quadrato del precedente.
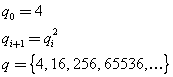
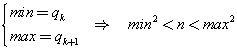
Esempio.
Sia n = 40401
Si ha 40401≡1 (mod 8) e 40401≡0 (mod 9): quindi il numero supera i due test preliminari proposti. Si applica l'algoritmo di bisezione
Un metodo più diretto di controllo della primalità è di un numero naturale, pure proposto da Fermat, si basa su un teorema enunciato da Fermat stesso, ma dimostrato successivamente da L. Euler, noto come Piccolo Teorema di Fermat.
Se p è primo, allora, per qualunque numero naturale n,
![]()
dove (mod p) rappresenta il resto della divisione per p.
Ad esempio: dati n=10 e p=3, si ha:
Una dimostrazione del teorema si può ottenere per induzione.
Prima di tutto si osserva che, se p è primo,
![]()
Infatti, sviluppando la potenza del binomio, si ha
![]()
dove
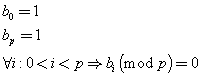
Ora si procede per induzione, osservando che il teorema vale per n=0 e n=1:
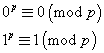
Assumendo il teorema valido per n
![]()
per la (1) si ha
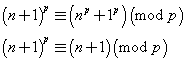
Quindi, per induzione, il teorema vale per ogni n.
In particolare, se n non ha divisori comuni con p, cioè è coprimo rispetto a p, si ha
![]()
Il teorema stabilisce una condizione necessaria, ma non sufficiente. Cioè qualunque primo p verifica il teorema,
ma possono esistere numeri composti c
che verificano la congruenza ![]() .
Questi numeri sono detti pseudoprimi di Fermat rispetto ad n.
In particolare, gli pseudoprimi rispetto a qualunque n coprimo con c sono detti
numeri di Carmichael.
.
Questi numeri sono detti pseudoprimi di Fermat rispetto ad n.
In particolare, gli pseudoprimi rispetto a qualunque n coprimo con c sono detti
numeri di Carmichael.
Quindi, se un numero q non verifica il teorema rispetto ad un coprimo n, si può affermare che q è composto, ma se lo verifica non si può affermare che esso è primo, ma solo che è, probabilmente primo.
Se si sperimentano molti valori n con esiti sempre positivi, si può operativamente assumere q come primo.
Esempi.
1. Sia q=41.
Si hanno così tre indizi indipendenti sulla primalità di 41, che è effettivamente primo come si può facilmente verificare.
2. Sia q=91.
3. Sia q=561.
Applicando il metodo di fattorizzazione di Fermat si ottiene 561=17·33. Dunque 561 è composto.
Si prova ora ad applicare il test di Fermat.
Il test di Fermat, anche con numerosi controlli, può fallire e indicare come primi numeri che invece sono composti.
Si può ridurre questo rischio e valutare la probabilità di ottenere una risposta corretta, osservando che perché un numero q>2, sia primo, q deve essere dispari e quindi q-1 è pari.
Ogni numero pari può essere scomposto nel prodotto di un numero dispari per una potenza di 2.
![]()
Dal teorema di Fermat, se q è primo e n coprimo con q,
![]() ,
si ha
,
si ha
![]()
da cui
![]()
quindi
![]()
Se questa radice è ≡ 1(mod q), allora la successiva sarà ≡ ±1 (mod q) e così via.
Se tutte le radici sono ≡ 1 (mod q), quindi anche nd≡1 (mod q), q supera il test ed è probabilmente primo.
Se la prima radice non ≡ 1 (mod q) è ≡ -1 (mod q), q supera il test ed è probabilmente primo.
In caso contrario q è composto.
In definitiva, per stabilire se q è probabilmente primo:
La probabilità che un numero composto q passi il test è al massimo ¼. Dunque, ripetendo il test con altri valori di n, la probabilità che q li superi tutti decresce esponenzialmente.
Esempi.
1. Come si è visto il numero q=561, pur essendo composto, supera il test di Fermat.
Si scompone 560 in prodotto tra un numero dispari e una potenza di 2: 560=35·24
Con n=2, si ha 235=34359738368; 235≡ 263 (mod 561)
35·23=280;
2280=1942668892225729070919461906823518906642406839052139521251812409738904285205208498176
2280≡1 (mod 561)
35·22=140;
2140=1393796574908163946345982392040522594123776
2140≡67 (mod 561)
Dunque 561 è composto.
2. Sia q=601
Con n=2, si ha
2600=414951556888099295851240786369116115101244623224243689999565732969065281141290814639970704894710379428
8197886611300789182395151075411775307886874834113963687061181803401509523685376
2600≡1 (mod 601): si supera il test di Fermat.
600=75*23
Con n=2 si ha
275=37778931862957161709568; 275≡ 1 (mod 601): 601 è probabilmente primo.
3. Sia q=401
Con n=2, si ha
2400=2582249878086908589655919172003011874329705792829223512830659356540647622016841194629645353280137831435903171972747493376
2400≡1 (mod 401): si supera il test di Fermat.
400=25·24
Con n=2 si ha
225=33554432; 275≡356 (mod 401)
2200=1606938044258990275541962092341162602522202993782792835301376; 2200≡ 1 (mod 401);
2100=1267650600228229401496703205376; 2100≡ -1 (mod 401): 401 è probabilmente primo.
Un numero naturale n o è primo o è composto.
Usando un test affidabile come quello di Miller-Rabin, si può decidere direttamente se è primo e quindi gli unici fattori sono 1 e n.
Se n è composto si può usare il crivello di Eratostene.
Tuttavia, se n è molto grande, anche √n è grande ed è grande anche il numero degli elementi di Qn il cui calcolo può richiedere tempi impraticabili.
In alternativa, con il metodo di Fermat:
Il metodo di Fermat funziona in modo soddisfacente per numeri non molto grandi o, anche per numeri grandi, se i due fattori h e k sono entrambi prossimi a √n. In caso contrario può comportare tempi di calcolo impraticabili anche sui sistemi più veloci.
Per superare queste difficoltà sono stati proposti altri metodi di fattorizzazione, come, ad esempio, il seguente algoritmo dovuto a John M. Pollard.
Sia h un divisore di n.
Se, dati s0 = a e la funzione f(s) = mod(s2+2,n), si costruisce la successione S in cui si+1 = f( si ), allora, dopo al massimo h+1 passaggi, si trova un ss tale che ss = sk (k > s) e quindi gli elementi successivi si ripetono ciclicamente. Rappresentando gli elementi come nodi di un grafo, questo assume una forma che ricorda la lettera greca ρ (trascrizione latina 'rho', corrispondente alla nostra r minuscola, da cui il nome dell'algoritmo).
Ad esempio, dato n = 51, h = 3 è un divisore di n. Posto s0 = 2, si ha
| i | si | f( si ) |
| 0 | 2 | 6 |
| 1 | 6 | 38 |
| 2 | 38 | 18 |
| 3 | 18 | 20 |
| 4 | 20 | 45 |
| 5 | 45 | 38 |
| 6 | 38 | 18 |
| 7 | 18 | 20 |
| 8 | 20 | 45 |
| 9 | 45 | 38 |
s2 = s6, quindi s3 = s7 e così via.
Se i ≠ j, sj > si e sj ≡ si (mod h), si ha:
e quindi
MCD ( sj - si , n ) = h
Se, continuando l'esempio proposto, si costruisce una tabella dei valori assoluti delle differenze di,j = si - sj tra tutti gli elementi sk calcolati, si osserva che, per i ≠ j, solo in alcuni casi il MCD(di,j,n) è maggiore di 1 e che in questi casi MCD = 3, cioè h.
| 2 | 6 | 38 | 18 | 20 | 45 | 38 | 18 | 20 | 45 | |
| 2 | 0 | 4 | 36 | 16 | 18 | 43 | 36 | 16 | 18 | 43 |
| 6 | 4 | 0 | 30 | 12 | 14 | 39 | 30 | 12 | 14 | 39 |
| 38 | 36 | 32 | 0 | 20 | 18 | 7 | 0 | 20 | 18 | 7 |
| 18 | 16 | 12 | 20 | 0 | 2 | 27 | 20 | 0 | 2 | 27 |
| 20 | 18 | 14 | 18 | 2 | 0 | 25 | 18 | 2 | 0 | 25 |
| 45 | 43 | 39 | 7 | 27 | 25 | 0 | 7 | 27 | 25 | 0 |
| 38 | 36 | 30 | 0 | 20 | 18 | 7 | 0 | 20 | 18 | 7 |
| 18 | 16 | 12 | 20 | 0 | 2 | 27 | 20 | 0 | 2 | 27 |
| 20 | 18 | 14 | 18 | 2 | 0 | 25 | 18 | 2 | 0 | 25 |
| 45 | 43 | 39 | 7 | 27 | 25 | 0 | 7 | 27 | 25 | 0 |
Quindi, scelti a caso si e sj con i ≠ j, MCD(di,j,n) > 1, allora MCD(di,j,n) = h.
Si possono evitare i tentativi casuali accostando ai termini della successione S con quelli della successione T in cui, dato t0 = 2, ti+1 = f( f( ti ) ).
Nell'esempio proposto:
| i | si | ti | | ti - si | |
| 0 | 2 | 2 | 0 |
| 1 | 6 | 38 | 32 |
| 2 | 38 | 20 | 18 |
| 3 | 18 | 38 | 20 |
| 4 | 20 | 20 | 0 |
| 5 | 45 | 38 | 7 |
| 6 | 38 | 20 | 18 |
| 7 | 18 | 38 | 20 |
| 8 | 20 | 20 | 0 |
| 9 | 45 | 38 | 7 |
Ovviamente l'insieme dei termini della successione T è un sottinsieme dell'insieme dei termini di S, quindi la differenza tra un termine di T e un termine di S è anche una differenza tra due termini di S. Accostando i termini delle due successioni e calcolando il massimo comun divisore tra n e il valore assoluto della differenza ti - si, se il massimo comun divisore è maggiore di 1, esso è un divisore di n cioè h.
Si può quindi calcolare k = n / h.
La seguente applicazione Javascript esegue i calcoli descritti.
Ovviamente, perché essa funzioni a dovere il vostro browser deve abilitare Javascript.
Se il vostro browser non permette i frames interni, potete accedere direttamente alla pagina dell'applicazione.
Se il tempo di calcolo supera i minuti indicati, potete provare ad aumentarli.
Le applicazioni di questa pagina sono redatte in JS e, per quanto potenziate dalla libreria BigInt di Leemon Baird, risultano inevitabilmente troppo lente per trattare numeri molto grandi. Dovendo scomporre in fattori numeri molto grandi si può ricorrere a WolframAlpha.
Va comunque osservato che, anche usando il software più evoluto e hardware appositamente progettato, la scomposizione in fattori di un numero molto grande può richiedere tempi di calcolo impraticabili e questo fatto è alla base dei metodi di crittografia più efficienti, come ad esempio la crittografia RSA.
ultima revisione: Giugno 2020