5. Intersezione tra due rette

Sulla base di quanto detto nei paragrafi precedenti si può dire che ogni equazione del tipo

rappresenta una retta nel piano cartesiano Oxy. Se a, b e c sono tutti non nulli, la retta non è parallela a nessuno degli assi; se a è nullo e b non è nullo, la retta è parallela all'asse delle ascisse; se b è nullo e a non è nullo la retta è parallela all'asse della ordinate.

L'equazione (5.1) è l'equazione di un luogo geometrico, rappresenta cioè l'insieme di tutti e soli i punti P(x;y) le cui coordinate verificano l'equazione. Un punto Q(x_Q;y_Q) appartiene a questo insieme se e solo se le sue coordinate x_Q e y_Q sostituite a x e y nella (5.1) azzerano il primo membro.

Considerate due rette r e r'  non parallele, ad ognuna di esse corrisponde una equazione del tipo (5.1).

Due rette non parallele, in geometria euclidea, hanno un sol punto in comune. Questo punto deve cioè appartenere ad entrambe le rette e quindi le sue coordinate devono soddisfare contemporaneamente le equazioni delle due rette.

Per determinare le coordinate di tale punto è quindi necessario risolvere il sistema formato dalle equazioni delle due rette. Sono noti vari metodi di risoluzione dei sistemi. Il più interessante in questa sede è il metodo di Cramer: supponendo che entrambe le rette non siano parallele ad uno degli assi e scrivendo il sistema nel seguente modo

la soluzione è data da

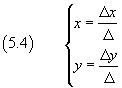
dove Δ rappresenta il determinante dei coefficienti delle variabili x e y, Δx rappresenta il determinante ottenuto dal precedente sostituendo la colonna dei coefficienti di x con la colonna dei coefficienti a secondo membro e Δy rappresenta il determinante ottenuto dal precedente sostituendo la colonna dei coefficienti di y con la colonna dei coefficienti a secondo membro:

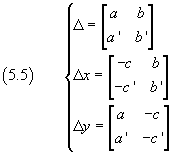
Nella (5.4) si osserva che perché il sistema sia determinato (abbia cioè una e una sola soluzione) bisogna che il denominatore Δ sia non nullo.

In caso contrario il sistema

• è impossibile se i numeratori sono non nulli: ciò significa geometricamente che le rette sono distinte e parallele;
• è indeterminato se anche i numeratori sono nulli: ciò significa geometricamente che le rette sono coincidenti.

Si può quindi concludere che condizione necessaria e sufficiente perché due rette distinte di equazioni (5.2) siano parallele è che sia nullo il determinante dei coefficienti delle variabili

Dalla (5.6) si evince che la condizione di parallelismo tra rette può essere enunciata anche nel seguente modo: condizione necessaria e sufficiente perché due rette distinte di equazioni (5.2) siano parallele è che i coefficienti corrispondenti delle variabili siano direttamente proporzionali.

Ricordando le (4.6)

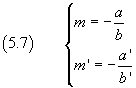
si può inoltre dire che condizione necessaria e sufficiente perché due rette distinte siano parallele è che abbiano coefficienti angolari uguali.

A quest'ultima conclusione si poteva giungere osservando che se due rette (non parallele all'asse delle ascisse) hanno uguale coefficiente angolare esse formano angoli corrispondenti uguali con l'asse delle ascisse e quindi sono parallele. Vale anche la proposizione inversa.

La seguente applicazione Javascript calcola le coordinate del punto di intersezione di due rette e disegna le rette nei dintorni del loro punto di intersezione, se esiste.
I valori in input possono interi, razionali rappresentati da frazioni, irrazionali in notazione decimale o espressi da costanti o funzioni (es. P, E, Sqrt[2], Sin(P/10), ecc.) e anche da espressioni.
L'applicazione funziona solo se il browser in uso permette i pop-up.