Per poter descrivere una retta r nel piano usando le coordinate polari in luogo delle più comuni coordinate cartesiane è anzitutto necessario stabilire un sistema di riferimento scegliendo un punto che funga da polo e una semiretta polare con origine nel polo.
Se si pone il polo sulla retta r stessa, qualunque sia la semiretta polare, tutti i punti di una semiretta di r avranno uguale anomalia α mentre i punti dell'altra semiretta avranno anomalia α + π e l'equazione di r risulterà semplicemente
r: (θ = α) V (θ = α + π) {α costante, 0≤α≤π}
Questa situazione è analoga a quella che si ha nei sistemi cartesiani per le rette parallele a uno degli assi.
Il modulo ρ può assumere qualunque valore non negativo.
Nell'ipotesi più generale che il polo sia scelto esternamente a r e che r formi in angolo γ (-π/2 ≤ γ ≤ π/2) rispetto alla semiretta polare, l'equazione polare della retta può essere dedotta da quella esplicita cartesiana quando si assuma il polo come origine del piano cartesiano e la retta contenente la semiretta polare come asse delle ascisse.
Da y = m x + q (q ≠ 0), ricordando le relazioni tra coordinate polari e cartesiane
x = ρ cos θ
y = ρ sin θ
si ha
ρ sin θ = m ρ cos θ + q
Esplicitando ρ in funzione di θ
Ricordando inoltre che m = tg γ si ha
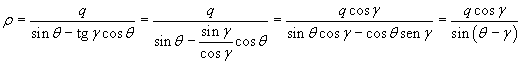
Inoltre
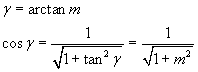
quindi
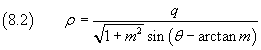
ρ non può essere negativo, quindi nell'espressione di ρ il denominatore sin(θ-γ) deve avere lo stesso segno del numeratore q. Inoltre 0 ≤ θ ≤ 2π. Si conclude quindi che:
se q è positivo
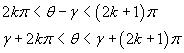
il valore minimo di ρ si ha quando il denominatore è massimo, cioè quando il valore di sin(θ-γ)=1; il valore minimo è quindi q cosγ;
se q è negativo
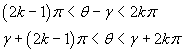
in questo caso il valore minimo di ρ è -q cosγ.
In entrambi i casi il valore minimo di ρ può essere espresso come
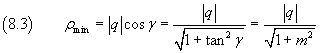
La (8.3) può essere usata per calcolare direttamente la distanza di un punto A(xA;yA) da una retta r: y = mx+q. Infatti, traslando l'origine O in A e mantenendo gli assi cartesiani paralleli, l'equazione della r diventa
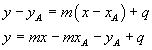
Detta H la proiezione ortogonale di A su r si ha
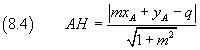
Esempi.
Per la retta di equazione cartesiana y = x + 1 si ha q = 1 e γ = π/4, dunque la sua equazione polare risulta
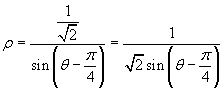
con 
La distanza della retta dal polo (origine del piano cartesiano) è data dal valore minimo di ρ:
.
Tale minimo si ha quando il denominatore della funzione è massimo, cioè quando il seno vale 1.
L'unica soluzione nel dominio è 
Per la retta di equazione cartesiana y =2 x - 3 si ha
q = -3 e γ = arctan 2 con 
,
dunque la sua equazione polare risulta
con 
La distanza della retta dal polo risulta 
Perché il seno a denominatore valga 1
L'unica soluzione nel dominio è 
Può essere un utile esercizio cercare l'intersezione tra le due rette proposte lavorando sulle loro equazioni polari.
A tale scopo conviene, nella seconda equazione, risostituire γ a arctan 2, ricordare che
il modulo di sin γ è 
e che la soluzione per θ deve appartenere all'intersezione tra i due domini.
La seguente applicazione Javascript calcola l'equazione polare di una retta dati il suo coefficiente angolare e la sua intercetta;
può calcolare anche il valore di ρ corrispondente ad una anomalia θ indicata.
I valori in input possono interi, razionali rappresentati da frazioni, irrazionali in notazione decimale o espressi da costanti o funzioni (es. P, E, Sqrt[2], Sin(P/10), ecc.)
e anche da espressioni.
L'applicazione funziona completamente solo se il browser in uso permette i pop-up.