in cui il naturale
i, detto indice e che definisce l'ordinamento, non può essere ripetuto,
mentre questa restrizione non vale per il reale a associato ad i, detto elemento i-esimo.Associando in un modo qualunque ad ogni numero naturale i, zero incluso, un numero reale a,
si ottiene un insieme ordinato di coppie
in cui il naturale
i, detto indice e che definisce l'ordinamento, non può essere ripetuto,
mentre questa restrizione non vale per il reale a associato ad i, detto elemento i-esimo.
L'insieme di queste coppie è detto successione di numeri reali e viene usualmente
denotato
o, più sinteticamente, 
.
Gli elementi ai della successione possono, come s'è detto, essere determinati in un modo qualunque, eventualmente anche con un generatore di numeri casuali, ad esempio, tirando un dado. In questa sede ci si interesserà solamente delle successioni in cui gli ai sono generati da un algoritmo prestabilito. Tali successioni saranno denominate successioni regolari.
Tali algoritmi possono essere di due tipi:
Un algoritmo intensivo è, sostanzialmente, una funzione, descrivibile analiticamente o con una procedura informatica, il cui esito dipende solamente dal valore dell'indice i.
Esempi.
Successione armonica
Successione oscillante
Successione di Nepero
Una funzione in Javascript
function esempio(i)
{
if (i%2==0)
return 1
else
return 1/i
}
...............
for (i=0; i<8; i++)
a[i] = esempio(i)
...............
Un algoritmo ricorsivo ricava un elemento dalla conoscenza di uno o più elementi precedenti. In questo caso per avviare l'algorimo è necessario predefinire uno o più elementi iniziali.
Esempi.
Successione aritmetica
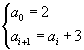
Successione di Erone
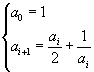
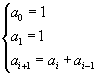
Gli elementi della successione di Fibonacci possono essere espressi anche in forma intensiva con la cosiddetta formula di Binet.
function collatz(i)
{
if (i%2==0)
return i/2
else
return 3*i+1
}
a[0] = 10
for (i=0; i<9; i++)
a[i+1] = collatz(a[i])
The On-Line Encyclopedia of Integer Sequences