5. Serie

5.1 Definizione

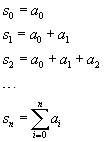
Data la successione {a_i} si dice serie la successione s delle somme s_n degli elementi di {a_i} con indici da 0 a n.

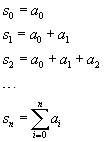
I numeri a_i sono gli elementi della serie, i numeri s_i sono i termini (o somme ridotte o, semplicemente ridotte) della serie.

Il limite di una serie viene usualmente indicato nel seguente modo

• Se il limite è un numero reale s, si dice che la serie converge.

  

• Se tutte le ridotte oltre un certo indice superano qualunque numero reale P positivo predefinito, si dice che la serie diverge positivamente.

  

• Se tutte le ridotte oltre un certo indice sono minori di qualunque numero reale N negativo predefinito, si dice che la serie diverge negativamente.

  

• In altri casi la serie è indeterminata.

5.2 Il teorema di Cauchy per le serie.

Condizione necessaria e sufficiente perché una serie converga è che, per qualunque ε reale positivo comunque piccolo, esista un indice m tale che, per qualunque coppia di indici h e k (h<k) entrambi maggiori di m, sia

Per le serie ciò equivale a

• Il modulo di una somma è minore o al massimo uguale alla somma dei moduli: dunque se la serie dei moduli degli elementi converge, cioè se la serie è assolutamente convergente, la serie converge.

• Se una successione è convergente, ci saranno sicuramente due indici successivi h e h+1 che verificano la disequazione: quindi se una successione è convergente, è necessario che per ogni i, da un certo m in poi,

  

  Ma questa condizione, pur necessaria, non è sufficiente a garantire che i moduli di tutte le somme di termini successivi a m siano minori di qualunque ε positivo prefissato.

  L'esempio tipico di questa situazione è dato dalla serie armonica, cioè dalla somma di tutti i reciproci dei numeri naturali:

  Infatti, comunque si fissi un reale positivo ε, si potrà trovare una frazione , ma potrà esistere una somma . Quindi la serie armonica non converge.

  Invece le serie costituite dalle somme dei reciproci delle stesse potenze con esponente naturale > 1 dei numeri naturali convergono. Si può dimostrare, ad esempio, che

5.3 Resto di una serie.

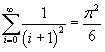
Data la serie a termini reali e fissato un indice r, la serie è detta resto r-esimo di A.

Detto σ il numero reale , si ha .

Dunque, A converge, diverge o oscilla se e solo se R converge, diverge o oscilla.