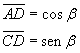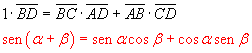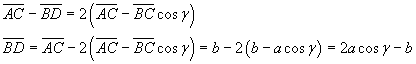Cliccare sui punti A, B, C, D per spostarli, evitando di alterare il loro ordinamento in senso antiorario.
Il teorema di Tolomeo
(a cura di Roberto Bigoni)
English version
Un teorema di geometria piana un po' trascurato nella didattica liceale corrente, ma che
invece può rivelarsi utile in varie situazioni, è il cosiddetto teorema di Tolomeo:
In un quadrilatero inscritto in una circonferenza, il prodotto delle misure delle diagonali
è uguale alla somma dei prodotti delle misure dei lati opposti.
Dimostrazione
Tesi: 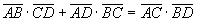
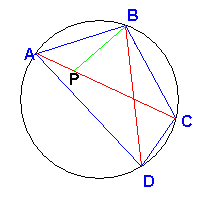
Scegliere sulla diagonale AC un punto P tale che l'angolo APB sia congruente con l'angolo
BCD. In questo modo si costruisce il triangolo APB che è simile al triangolo BDC.
Infatti anche gli angoli BAP e BDC sono congruenti in quanto sono angoli alla circonferenza
che insistono sullo stesso arco BC.
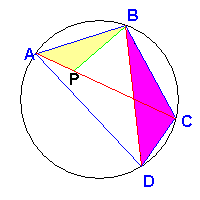
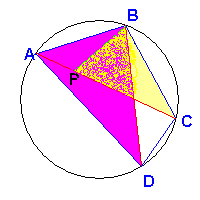
I lati corrispondenti sono proporzionali, quindi
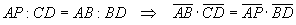
Anche i triangoli BPC e ABD risultano simili perché gli angoli PBC e ABD sono congruenti
in quanto somme di angoli uguali e PCB e ADB sono congruenti in quanto insistono sullo stesso
arco AB.
I lati corrispondenti sono proporzionali, quindi
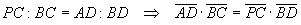
Sommando membro a membro le uguaglianze di prodotti ottenuti si ottiene la tesi.
Il teorema di Tolomeo è una generalizzazione del teorema di Pitagora.
Infatti ogni rettangolo è un quadrilatero inscrivibile nella circonferenza con un diametro
coincidente con una delle sue diagonali.
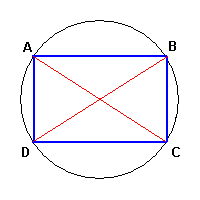
Applicando il teorema di Tolomeo al rettangolo ABCD, dato che i lati opposti e le diagonali
sono congruenti, si ottiene immediatamente
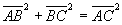
cioè nel triangolo rettangolo ABC la somma dei quadrati delle misure dei cateti è uguale
al quadrato della misura dell'ipotenusa.
Si consideri il quadrilatero ABCD inscritto inscritto in una circonferenza di diametro
unitario e tale che la diagonale AC coincida con un diametro.
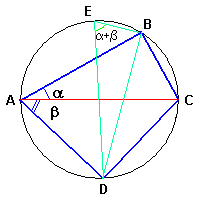
Il triangolo ABC è rettangolo: dunque
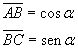
Il triangolo ACD è rettangolo: dunque
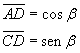
Si tracci il diametro DE e quindi la corda EB. Il triangolo DEB è rettangolo e l'angolo
acuto DEB è congruente con l'angolo BAD poiché entrambi sono angoli alla circonferenza
che insistono sullo stesso arco BD. Risulta quindi
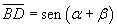
Applicando il teorema di Tolomeo al quadrilatero ABCD si ottiene
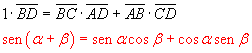
Questa è la formula di addizione per il seno da cui possono essere dedotte
molte altre identità sulle funzioni circolari.
Si consideri un triangolo qualunque ABC, i cui lati misurino rispettivamente
a, b e c;
si tracci la circonferenza ad esso circoscritta
e si tracci da un suo vertice, ad esempio B, la parallela al lato opposto che interseca
la circonferenza in D; si chiuda infine il quadrilatero tracciando il segmento DC.
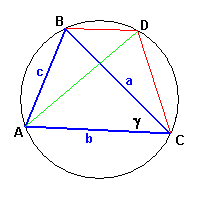
Il quadrilatero ABDC è un trapezio isoscele, in cui i lati obliqui e le diagonali sono
congruenti ed hanno quindi uguale misura.
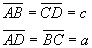
Si ha inoltre
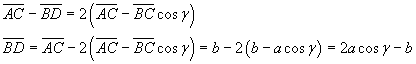
Applicando il teorema di Tolomeo si ottiene
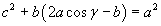
e infine
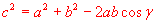
Si è ottenuta una notevole relazione tra i quadrati dei lati di un triangolo qualunque
che generalizza il teorema di Pitagora.
In un triangolo qualunque il quadrato della misura di un lato è uguale
alla somma dei quadrati delle misure degli altri due meno il doppio del loro prodotto per
il coseno dell'angolo tra essi compreso.
Questa relazione è nota come
Teorema di Carnot o
Teorema del coseno.
ultima revisione: 05/06/2015
![]()


![]()

![]()