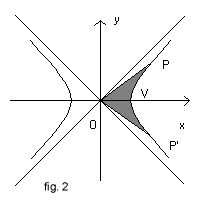
Dati nel piano cartesiano Oxy il grafico dell'iperbole equilatera δ con centro nell'origine O
e semiasse reale unitario, di equazione
,
siano V il punto in cui δ interseca il semiasse positivo delle ascisse, P(x;y) un suo punto qualunque e
P' il punto di δ simmetrico di P rispetto all'asse delle ascisse.
Come nel caso della circonferenza considerato nella sezione precedente, le coordinate x and y di P possono essere espresse come funzioni parametriche dell'area α del settore iperbolico OPVP'.
Queste funzioni sono dette rispettivamente coseno iperbolico e seno iperbolico di α.
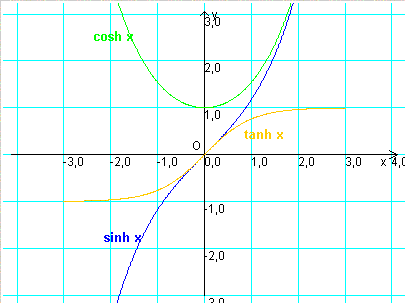
Dall'equazione di δ si ha
Il rapporto tra seno e coseno iperbolici è detto tangente iperbolica
Si può osservare che
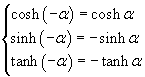
Il coseno è una funzione pari, mentre il seno e la tangente sono funzioni dispari, quindi il grafico del coseno è simmetrico rispetto all'asse delle ordinate, i grafico del seno e della tangente sono simmetrici rispetto all'origine.
La seguente applicazione Javascript permette il calcolo dei valori delle tre funzioni.
Se il browser attivo non accetta il tag iframe è possibile accedere direttamente alla pagina.
Quanto più P si avvicina a V, tanto più il settore iperbolico circolare OPVP' diventa indistinguibile da un triangolo isoscele di altezza OV=1 e base PP' = 2sinhα. In un triangolo il rapporto tra il doppio dell'area e la base è uguale all'altezza, per cui
Se si muove il punto P lungo δ aumentando l'area α fino a che diventa
α+β, si arriva ad un punto Q(X;Y) di δ tale che
, dove
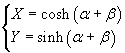
Se si applica al punto P(x;y) di δ la trasformazione
si ottiene proprio
, quindi
la trasformazione (2.5) trasforma il punto P nel punto Q.
In generale, trasformazioni del tipo (2.5) trasformano una iperbole equilatera in se stessa. Queste trasformazioni sono dette rotazioni iperboliche.
Quindi
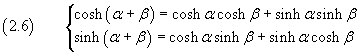
Le (2.6) sono le formule di addizione per il coseno e il seno iperbolici.
Formule di addizione con WolframAlpha.
In modo del tutto analogo a quanto visto per le funzioni circolari, dalle formule di addizione si deducono agevolmente altre utili identità come le formule di duplicazione
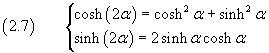
Formule di duplicazione con WolframAlpha.
e le formule di prostaferesi
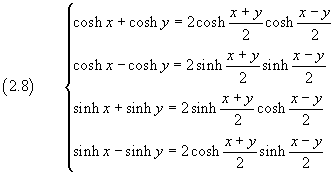
Formule di prostaferesi con WolframAlpha
La derivata di sinh x rispetto a x, per definizione, è
Per la quarta formula di prostaferesi il numeratore è
quindi
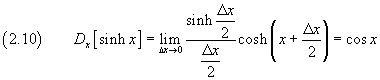
La derivata di cosh x rispetto a x, per definizione, è
Per la seconda formula di prostaferesi il numeratore è
quindi
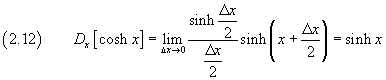
La derivata di tanh x rispetto a x si ottiene derivando il quoziente tra seno e coseno
Note le derivate delle funzioni iperboliche dirette, č immediatamente possibile risalire alle antiderivate delle derivate, cioč ottenere gli integrali indefiniti delle derivate.
