10. Le funzioni come vettori.

Gli elementi di qualunque insieme su cui si possa operare in modo analogo a quello in cui si opera sulle ennuple di numeri reali possono essere essere a tutti gli effetti considerati vettori.

Questa affermazione può essere verificata in particolare per insiemi di funzioni di forma assegnata.

Si consideri, ad esempio, l'insieme Σ₂ delle funzioni di forma con a e b numeri reali qualsiasi e definite per x ∈ [-π ; π]. Per semplicità di notazione, queste funzioni saranno in seguito indicate con σ₂(a,b).

Due qualunque funzioni di Σ₂ si possono si possono sommare con gli usuali metodi dell'algebra ottenendo una funzione di Σ₂, quindi la somma è interna. La somma è associativa e commutativa. La funzione nulla è ovviamente σ₂(0,0) e per ogni σ₂(a,b) esiste in Σ₂ l'opposta σ₂(-a,-b). Dunque Σ₂ con l'operazione di somma è un gruppo commutativo.

Le σ possono essere moltiplicate per un reale k ottenendo sempre una funzione di Σ₂.

In generale si può osservare che, date due funzioni σ₂(a,b) e σ₂(c,d)

Per il calcolo di questo e di altri integrali può essere utile The Wolfram Integrator

Il valore di questo integrale coincide a meno del fattore costante π con quello del prodotto scalare tra i vettori reali piani (a,b) e (c,d). Appare quindi sensato definire in generale come prodotto scalare di σ₂(a,b) per σ₂(c,d), denotandolo con <σ₂(a,b)|σ₂(c,d)>, l'integrale

Questa definizione di prodotto scalare permette a sua volta di definire la norma ||σ₂(a,b)|| delle funzioni σ₂(a,b), analoga al modulo di un vettore reale

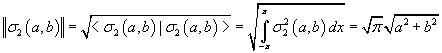
Si può quindi dire che l'insieme Σ₂, come l'insieme dei vettori reali piani, è uno spazio vettoriale normato e i suoi elementi σ₂(a,b) possono essere detti vettori.

Un operatore lineare L su questo spazio vettoriale deve essere tale da far corrispondere in modo univoco ad ogni vettore un vettore dello stesso spazio e godere delle stesse proprietà di cui godono le matrici reali quadrate rispetto ai vettori reali piani evidenziate nel paragrafo 2, cioè

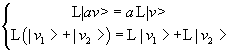
La derivata seconda delle funzioni di Σ₂ rispetto alla variabile x ha tutte queste proprietà: infatti la derivata di una somma di funzioni è la somma delle derivate delle singole funzioni e la derivata del prodotto di una funzione per un numero reale k è uguale al prodotto di k per la derivata della funzione. Inoltre

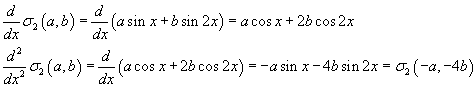
L'operatore di doppia derivazione è quindi un operatore lineare sullo spazio vettoriale Σ₂. Per l'individuazione dei suoi autovalori e dei suoi autovettori (che in questo caso sono le sue autofunzioni) bisogna risolvere l'equazione

cioè

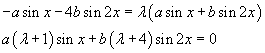
Questa equazione può essere soddisfatta solo se

Dunque gli autovalori dell'operatore considerato sono λ₁=-1 e λ₂=-4 e le corrispondenti autofunzioni sono σ₁=a sinx e σ₂=b sin2x.

Come si è osservato nel paragrafo precedente, gli autovalori risultano determinati a meno di una costante moltiplicativa. Può essere utile 'normalizzarli' assumendo a e b positivi e dividendoli per la loro norma. Si ottiene

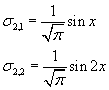
σ_2,1 e σ_2,2 costituiscono una base ortonormale dello spazio vettoriale considerato: ognuno di essi ha norma 1 e il loro prodotto scalare è nullo. Tutti i vettori dello spazio vettoriale Σ₂ si ottengono da combinazioni lineari di questi due vettori allo stesso modo in cui tutti i vettori piani reali possono essere ottenuti come combinazioni lineari dei vettori (1,0) e (0,1).

Considerando l'insieme Γ₂ delle funzioni di forma definite sull'intervallo reale [-π ; π] si giunge a conclusioni del tutto analoghe.

L'analogia permane anche per l'insieme Φ₂ delle funzioni di tipo per le quali si ha . Anche in questo caso l'integrale genera un valore che, a meno del fattore costante π, corrisponde al prodotto scalare dei due quadrivettori (a,b,c,d) e (h,k,l,m).

Per induzione si può concludere che Φ_n, cioè l'insieme delle funzioni di tipo , è uno spazio vettoriale normato, con norma definita da .

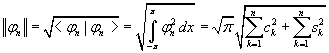In particolare, per ogni coppia di funzioni 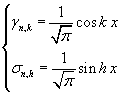si ha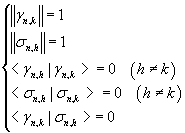

Quindi l'unione degli insiemi delle funzioni costituisce una base ortonormale dello spazio vettoriale Φ_n e ogni funzione di Φ_n può essere espressa nel seguente modo

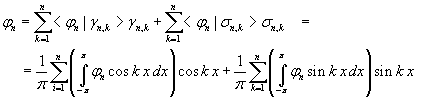
In definitiva, ponendo

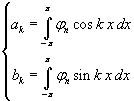
si ha