5. Operatori lineari in geometria analitica.

Interpretando i punti di un piano cartesiano come vettori, un operatore lineare invertibile, rappresentato da una matrice quadrata bidimensionale, determina una corrispondenza del piano in sé detta trasformazione lineare geometrica piana.

Queste trasformazioni godono di notevoli proprietà.

• Un operatore lineare trasforma l'origine in se stessa.

  

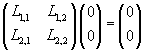
• Dato nel piano cartesiano Oxy il triangolo τ di vertici A(x_A;y_A), B(x_B;y_B), C(x_C;y_C) orientati in senso antiorario, il doppio dell' area di tale triangolo risulta

  

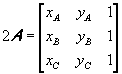
  Una trasformazione lineare 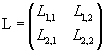trasforma il triangolo in un triangolo t’ di doppia area

  

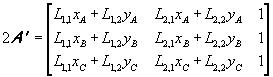
  Il determinante ottenuto è il prodotto dei determinanti

  

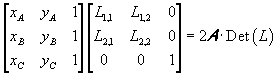
  quindi

  

  Una trasformazione lineare L trasforma un triangolo τ di area A in un triangolo τ' di area A' uguale al prodotto di A per il determinante di L.

  • Dato il significato geometrico dell'area, se il determinante è negativo, va considerato in valore assoluto.
  • Poiché ogni poligono è scomponibile in triangoli il teorema può essere esteso a tutti i poligoni.
  • In generale il teorema può essere esteso a tutte le figure piane.
  • Se tre punti sono allineati (cioè il triangolo da essi individuato ha area nulla) anche i tre punti trasformati sono allineati: quindi una trasformazione lineare trasforma una retta in una retta.

   

• Si considerino due rette tra loro parallele ma non parallele agli assi coordinati. La prima intersechi gli assi nei punti U(p ; 0) e V(0 ; q), la seconda nei punti R(kp ; 0) S(0 ; kq).

  Applicando a tali punti la trasformazione lineare 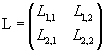si ottengono i punti corrispondenti

  

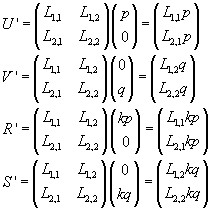
  I coefficienti angolari delle due rette trasformate risultano uguali.

  Quindi una trasformazione lineare trasforma rette parallele in rette parallele.

  Una trasformazione lineare trasforma parallelogrammi in parallelogrammi.