Un vettore può ammettere multipli e sottomultipli.
Dato il vettore v, il suo multiplo di ordine m è indicato con mv;
il suo sottomultiplo di ordine n è indicato con
![]()
il multiplo di ordine m del sottomultiplo di ordine n è indicato con
![]()
E' possibile quindi parlare del prodotto di un vettore per un numero razionale e più in generale per un numero reale, che in questo contesto è detto scalare.
Il prodotto di un vettore per uno scalare è un vettore di uguale direzione e verso di quello moltiplicato e di intensità data dal prodotto della sua intensità per lo scalare.
Dato un vettore v, sia
![]() il suo modulo. Allora il vettore
il suo modulo. Allora il vettore
![]() ha modulo 1.
ha modulo 1.
Il vettore uv, di modulo unitario e direzione e verso coincidenti con quelli di v, è detto versore di v.
In generale, un versore è un vettore di modulo 1.
Due vettori ordinati a e b applicati allo stesso punto O individuano un angolo convesso θ. Sia α il piano di questo angolo. Si può rappresentare la rotazione che porta a a sovrapporsi a b, percorrendo θ in verso antiorario, con un versore perpendicolare ad α e diretto verso l'osservatore. Tale versore è detto versore di rotazione.
Se si scambiano a e b, il che è come dire che l'osservatore è posto nel semispazio opposto rispetto ad α e vede la rotazione in senso orario, il versore di rotazione risulta di verso opposto a quello precedente, cioè va dall'osservatore ad α.
Due vettori a e b applicati allo stesso punto O individuano un parallelogramma di lati corrispondenti ai moduli dei due vettori. Il il vettore v risultante dal prodotto di quest'area per il versore di rotazione da a e b è detto prodotto vettoriale di a per b e viene indicato con
![]()
o anche con
![]()
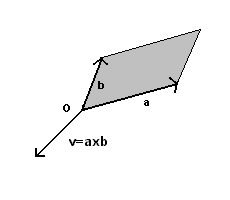
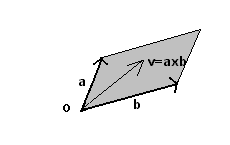
Il prodotto vettoriale non è commutativo. Invertendo l'ordine dei fattori, modulo e direzione rimangono uguali ma il verso si inverte: si ottiene cioè il vettore opposto. Si dice quindi che il prodotto vettoriale è anticommutativo
Il prodotto vettoriale di due vettori paralleli (equiversi o no) è nullo. In particolare il prodotto vettoriale di un vettore per se stesso è nullo.
Il modulo del prodotto vettoriale è massimo quando i vettori sono perpendicolari.
L'area di un parallelogramma coincide con quella del rettangolo di ugual base e uguale altezza. Considerando il modulo del vettore a come base e conoscendo la misura dell'angolo convesso θ formato dai due vettori, l'altezza del rettangolo è b sen θ: il modulo del prodotto vettoriale risulta quindi
![]()
Si definisce prodotto scalare di due vettori a e b l'area del rettangolo che ha per lati il modulo di uno di essi e il modulo della proiezione dell'altro sulla direzione del primo. L'area, e quindi il prodotto scalare, si considera positiva se la proiezione è equiversa con il vettore, negativa in caso contrario.
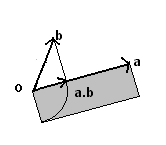
Il prodotto scalare è un numero reale (da cui il nome di 'scalare').
Se l'angolo tra i due vettori è acuto, il prodotto scalare è positivo: se l'angolo è ottuso, la proiezione risulta di verso opposto a quella dell'altro vettore e il prodotto scalare è negativo.
Il prodotto scalare è commutativo.
Il prodotto scalare di due vettori perpendicolari è nullo.
Il modulo del prodotto scalare di due vettori è massimo quando i vettori sono paralleli.
Se si conosce l'angolo θ formato dai due vettori applicati allo stesso punto, la proiezione di un vettore sulla retta dell'altro si ottiene moltiplicando il suo modulo per il coseno di θ.
Il prodotto scalare s dei vettori a e b risulta quindi
![]()
Il quadrato di un vettore è dato dal prodotto scalare del vettore per sè stesso. Il quadrato di un vettore è quindi uno scalare dato dal quadrato del suo modulo.