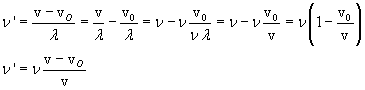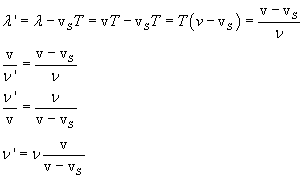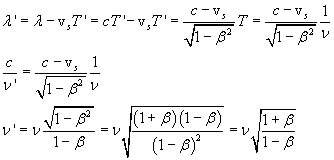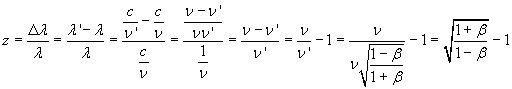Doppler effect
notes by R. Bigoni
1. Doppler effect in acoustics.
Sound waves are longitudinal waves that propagate in the air
(or other elastic medium), with speed, relative to the medium, depending only on the physical characteristics
of the medium itself.
If the source S and the observer O are both at rest with respect to a reference frame anchored to the medium,
O perceives waves with frequency ν identical to that of S.
But if S or O or both are moving with respect to the medium, O perceives a frequency ν'
different from ν.
This variation of the frequency ν' perceived by O with respect to the frequency ν emitted by S
is called Doppler effect.
-
Source at rest - Observer moving.
Denoting by v the velocity of the wave with respect to the medium and by vO
the speed of O with respect to the same medium, the waves, with respect to O, have speed
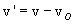
We apply the Galilean composition of velocities because v is much smaller than the speed of light c.
Of course, if vO is positive like v and greater than v, O will never be reached
by the waves. So we assume vO<v.
In Galilean relativity, observers that move relative to each other, measure the same lengths,
then O perceives the wave with the same length λ the wave has with respect to the medium,
but perceives the frequency
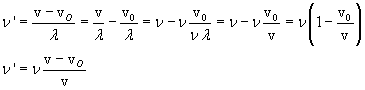
If O is moving away from S, it perceives frequencies less than those it which would receive if it were at rest;
conversely, if it is approaching S, it perceives higher frequencies, because in this case vO
is negative.
-
Observer at rest - Source moving.
If S is approaching O with velocity vS, O does not observe changes in wave
velocity with respect to v, as it did in the previous case, because it is at rest with respect to the medium,
but it perceives the distance between two successive wave fronts, that is the wave length, lower than it would perceive
if the source was at rest, because between the emission of two successive wavefronts
the distance of S from O has a decrease of vST. So:
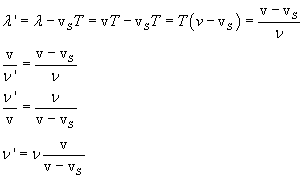
If S is approaching O, O perceives a a frequency greater than that it would receive if S were at rest;
conversely, if S is moving away, O perceives a lower frequency, because in this case vS is negative.
The following Javascript application simulates the Doppler effect in acoustics.
The application generates sounds, so it is effective only in systems with recording sounds (speakers, headphones, ...).
The speed of sound is conventionally fixed at 340 m/s.
The application allows to establish the frequency of the sound emitted by a source, the speed of the source and of the observer
with respect to air, assumed to be stationary, and the duration of the sound in seconds.
All these values can be represented by real numbers.
The two speeds can be positive or negative. They are positive if they are directed to the right, negative otherwise.
The source is assumed to be to the left of the observer: thus, for example:
- if the observer is at rest and the source has positive velocity, the source approaches the observer;
- if the observer is at rest and the source has negative velocity, the source moves away from the observer;
- if the source is at rest and the observer has positive speed, the observer moves away from the source;
- if the source is at rest and the observer has negative velocity, the observer approaches the source;
2. Doppler effect in optics.
For the fundamental principle of Special Relativity,
the speed of light and of any other electromagnetic wave, in vacuum has speed c that is the same for all observers,
regardless of the relative motion of each other.
Therefore, it cannot happen that an observer O, as it was admitted into the first of the cases considered above,
observes light waves having a speed different from c.
In other words, we can not take into account the motion of O or of S with respect a medium
(the hypothesized the ether does not exist); we can only consider the relative motion of S with respect to O
(or, optionally, of O with respect to S).
Therefore, the only acceptable situation is the second one of those examined above in the case of acoustic waves;
but we must to take in account that, for the time dilation, if a phenomenon has duration T with respect to S
and S is moving with velocity vS with respect to O, then the same phenomenon, with respect to O,
has duration
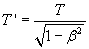
So, with respect to the frame reference O, we have
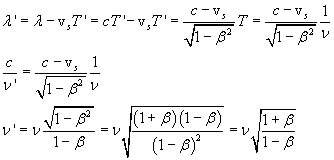
If S approaches O (vS>0), O perceives a higher frequency than it would perceive
if S was motionless with respect to itself.
This means, for example, that if some atom, in laboratory frame of reference, produces a set of spectral lines,
the spectral lines of the same atom, if it is on a star that is approaching (or which we are approaching),
are higher than those observed in a steady source. This phenomenon is known as blueshift.
If instead the source moves away, the observed frequencies are lower than those observed in a steady source:
we observe a redshift.
Conversely, if a source shows redshift, it is moving away. By measuring the redshift,
we can calculate the speed with which the source moves away.
Given the magnitude of the speed, when there is redshift we have
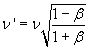
Usually the intensity of the redshift is measured by the parameter z:
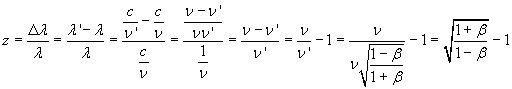
last revision: October 2015
![]()