.
They can be idealized as consisting of infinitely many infinitesimal elements with infinitesimal volume
d and infinitesimal mass dm.
The density ρ of each of these elements isCommon physical bodies have extension, so they are characterized not only by their mass m, but also from
their volume
.
They can be idealized as consisting of infinitely many infinitesimal elements with infinitesimal volume
d and infinitesimal mass dm.
The density ρ of each of these elements is
then
If ρ is constant, ie if the body is homogeneous,
If the infinitesimal mass dm, located at the point O, interacts with the adjacent small masses so that a displacement from its rest position is countered by a force opposing to the displacement and directly proportional to it, that is by an elastic force, the mass reacts to this displacement with a harmonic motion. In turn, this displacement, due to its interaction with the adjacent masses, causes a displacement of these masses from their rest position and thus they begin to oscillate with harmonic motion.
This is what happens, for example, when a stone hits a point O on the still surface of a pond. The point O, displaced from its rest position by the impact of the stone, after the sinking of the stone is subjected to a reaction opposed to the displacement due to surface tension and intermolecular forces, and begins to oscillate with harmonic motion. After a short time, any other point P on the surface of the pond will fluctuate with harmonic motion, as can be verified by observing the motion of any small object floating on the surface of the pond.
The oscillation phenomenon affecting all the points of the surface of the pond is called sine wave.
In the example of waves in the pond, the surface of the pond is the medium of wave propagation. The sets of contiguous points of the surface which oscillate in phase, ie that at any time have the same level, are circles said wavefronts. The smallest distance between two wavefronts whose points oscillate in phase with each other is called wavelength. The point O, center of the wavefronts, is called source of the wave.
The harmonic motion of the point O is described by the variation over the time of its displacement zO with respect to the undisturbed surface of the pond. With a suitable choice of the origin of time, zO varies over time according to the law
where A, the amplitude, in this case represents the greatest distance of the point O from its rest position.
If we assume that O can maintain over the time its amplitude and that the medium is perfectly elastic, at any other point P, at distance r from O, after a time t, depending on r and on the magnitude of the constant velocity v of propagation of the perturbation, the position z of P with respect to the undisturbed surface of the pond will begin to oscillate with harmonic motion, but delayed with respect to O. The delay will be greater the greater the distance r from O and less the greater the velocity v.
Therefore z varies over time with a trend expressed by
In general, what happens to the position of a point on the surface of a pond can occur for other scalar o vector variables, which later will be denoted by the symbol Ψ, time-varying functions of the position of a point P of a continuous medium, when P is reached by a perturbation generated by a source S at distance r from P and propagating with constant velocity v.
animation
In the case where Ψ is a scalar quantity or vector quantity parallel to the propagation velocity v, the wave is called longitudinal.
animation
Instead, if Ψ is a vector perpendicular to v, the wave is said transverse.
animation
In the case of transverse waves, it is often important to evaluate the angle between the plane containing the vector Ψ and the velocity v, said polarization plane, and a fixed reference plane. This angle is called polarization angle and can be constant or rotate during propagation of the wave.
It should also be noted that the propagation speed depends only on the characteristics of the medium and is therefore completely independent from the source. For example:
(T: tension; μ:linear density)
(γ: ratio cp/cv; p: pressure;
ρ: density
(B: bulk modulus; ρ: density)
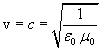(ε0: dielectric constant;
μ0: magnetic permeability)
In general, the point P is a point in a three-dimensional medium, so the wavefronts (assuming a homogeneous and isotropic medium) are spherical surfaces.
The trend of quantity Ψ, in a way analogous to that of the quantity z in the equation of (3.5), is expressed by
The equation (3.6) is said wave equation.
Using in the equation (3.6) the expression of ω in (2.10) we obtain
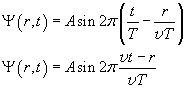
The product vT coincides with the wavelength λ
so we have
The wave function Ψ can be expressed in a more concise and significant way as
where the parameter
is called wavenumber.
From the equations (3.7) and (3.9) we obtain
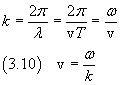
To learn more: Doppler effect.
If we calculate the second derivative of the wave function in the equation (3.8) with respect to time, we obtain
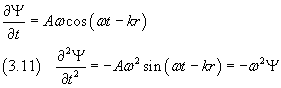
In the equation (3.6) the scalar r is the distance of a point P from the source O. If the cartesian coordinates of P arex, y, z, we have
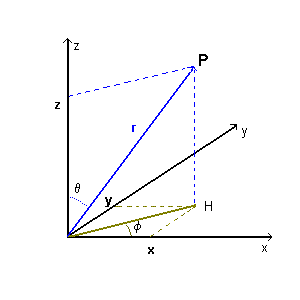
The first partial derivative of Ψ with respect to x is
Since
with θ and φ constant because the wave propagation is radial, we have
The second partial derivative with respect to x, is
Similarly we can calculate the second partial derivatives of Ψ with respect to y and z
If we sum the equations (3.12), (3.13) and (3.14) we obtain
Introducing the differential operator
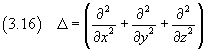
said Laplacian, we can rewrite the equation (3.15) as
From the equations (3.11) and (3.17) we obtain
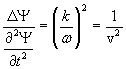
and finally
The equation (3.18) is known as wave equation or D'Alembert's equation. Thus, a sine wave function satisfies the D'Alembert's equation.
Conversely, every function that satisfies the D'Alembert's equation is a wave function.
Sometimes, to get a more concise expression of d'Alembert's equation, one may use the operator
said d'Alembertian, so that the equation (3.18) simply becomes
If we assume that at the initial instant the value of a sine wave function, at the point where the source is, has its maximum, then the function is expressed by
Since
,
we can interpret the expression (3.21) as the real part of the complex function
In the description of the waves we can use directly the expression (3.22) obtaining, in many situations, significant advantages in exposure and processing.
A point P of mass dm which oscillates harmonically with amplitude A and angular frequency ω, from the equation for (2.13), has total energy
If we consider the infinitesimal volume
d of the spherical shell centered
on the source O and having radius r and thickness dr
from the equation (3.23) we obtain
If we divide both sides of the equation (3.24) by dt, we have
The left hand side in (3.25) is the power through a the spherical surface with radius r, that is the amount of energy crossing the surface per unit time.
If we divide the right hand member of (3.26) by the surface of the spherical wavefront
, we obtain
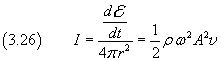
The quantity I represents the amount of energy that hits the unit area per unit time and is called intensity.
Introducing the quantity
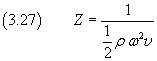
said impedance, the intensity can be expressed as follows
