.
Nevertheless, to understand the mechanical behavior of extended bodies, we can think of them as made by
an infinite number of point bodies, each of them having infinitesimal mass dm and infinitesimal volume
d, so that their density ρ is Real physical bodies, unlike theoretical point bodies, have not only mass m but also extension,
measured by their volume
.
Nevertheless, to understand the mechanical behavior of extended bodies, we can think of them as made by
an infinite number of point bodies, each of them having infinitesimal mass dm and infinitesimal volume
d, so that their density ρ is
that is
If ρ is constant, that is the body is homogeneous,
If the infinitesimal mass dm, placed at the point O, interacts with contiguous infinitesimal masses in a way such that a displacement from O is countered by a force proportional and opposite to the displacement, that is by an elastic force, the mass dm, when displaced, swings with harmonic motion. This motion displaces the contiguous masses which begin to swing with identical harmonic motion, but delayed by a time depending on their distance from O and on the internal structure of the body.
This is what happens, for example, when a stone hits a point O on the still surface of a pond. The point O, displaced from its position of balance by the impact of the stone, after the sinking of the stone, is subject to forces opposite to the displacement, due to surface tension forces and intermolecular forces, and begins to swing with harmonic motion. After a time, every other point P of the surface of the pond fluctuate with harmonic motion, as can be verified by observing the motion of any small object floating on the surface of the pond.
The phenomenon of oscillation that invests all points of the surface of the pond is called sine wave. The surface of the pond is the propagation medium of the wave. The sets of the contiguous points of the surface that swing in phase, that is the points that at every instant have the same displacement, are circumferences called wavefronts. The smallest distance between two wavefronts that oscillate in phase is called wavelength. The point O, from which the wavefronts start, is the source of the wave.
In the example, the harmonic motion of O is described by the temporal trend of its displacement zO from the still surface of the pond
where A, the amplitude, is the greatest displacement from the untroubled surface.
If we admit that O can keep its amplitude for a long time and that the medium is perfectly elastic, every other point P of the surface, at a distance r from O, after a time Δt = r/v, where v is the constant speed v at which the disruption spreads, starts swinging with same amplitude and angular frequency as O. The height z of a point P, with respect to r and t is
In general, what happens to the height of a point on the water surface can happen to many other scalar or vector physical quantities whose values (magnitude and/or direction, if vectors) depend on position. Such quantities are said fields. In the proposed example, the water surface is a field of altitudes.
When the value of a field Ψ at the point P with position r(x,y,z) changes with the time like the altitude of a point on the pond surface, we say that there is a wave
The (3.6) is said wave equation.
With the value of ω given in (2.10) we have
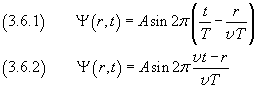
The product vT represents the distance covered by a wavefront in one period T: this is the wavelength λ
We can write
You can see some maybe useful animations in Waves.
If we now remember the expression (2.13) of the total energy of a harmonic oscillator and apply such equation to a mass dm of a material one-dimensional medium harmonically swinging with amplitude A and angular frequency ω, we have
Let the infinitesimal volume
d of the considered mass be that of a
spherical shell with center in the source O, radius r and thickness dr
From (3.8) we have
If we divide both the sides by dt we have
The first side of (3.10) shows that the spherical surfaces of the shell are crossed by energy. But the mass dm does not move. It oscillates, but its mean position is constant.
Therefore the equation (3.10) highlights that when a wave spreads within a medium there is propagation of energy without motion of mass.
By comparing this result and that obtained in section 1, we see that the energy can propagate from a source to the surrounding space in two fundamental ways:
These two ways differ greatly from each other for a fundamental reason: two waves, emitted from two different sources, may overlap without reciprocal interaction in the same point of the medium. In this case the mechanical behavior of the point is forced simultaneously by both the waves, but the waves go on without any change to their nature, as they were alone. This phenomenon is said interference. To the contrary, two particles can not coexist in the same point in space: the more they approach each other, the more they interact with changes in their momenta and energies. They do not interefere, they collide.
Physicists in 18th and 19th centuries, faced with phenomena of propagation of energy like, for example, emission of light from a gas or of radiation from a cathode, asked themselves whether such phenomena were carried by waves or particles, considering incompatible, mutually exclusive, the two modes.
Light was reckoned to be an ondulatory phenomenon, according to the opinion of Huygens and in opposition to the opinion of Newton, because Young and other physicists observed that two beams of light can interfere to enhance or reduce the light intensity. Cathodic rays instead were interpreted as formed by particles called electrons.