An optical property of the focus.

(notes by R. Bigoni)

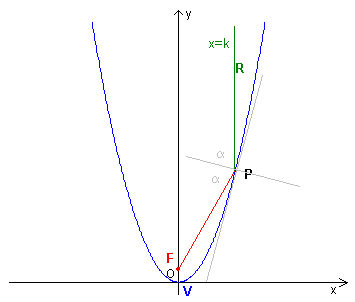
Given in a cartesian orthogonal plane Π the parabola γ of equation and the straight line r of equation , let F be the focus of γ, P the the point where the two curves intersect each other, R a point of r such that, if a>0, y_R > y_P, otherwise y_R < y_P

It can be demonstrated that the bisector of the salient angle FPR coincides with the normal to γ in P. (The normal is the perpendicular to the line tangent to γ in P.)

The coordinates of F are and those of P are , so the equation of the straight line FP is

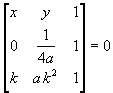
By expanding the determinant one obtain

The equations of the bisectors of the angles formed by the lines FP and PR are

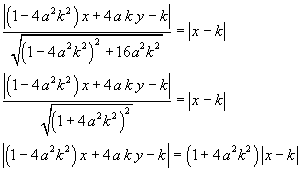
This equation is equivalent to the following pair

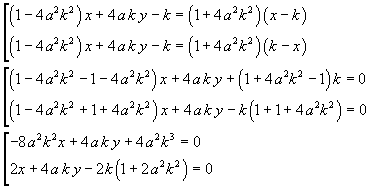
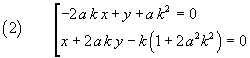
As we could expect, the two bisectors result perpendicular because the product of their slopes is -1.

By applying the doubling rule, the tangent to γ in its point P is

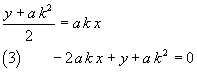
The (3) coincides with the first one in the (2), so the (2) are the equations of the tangent and the normal to γ in P. Therefore the angles formed by the lines FP and RP with the normal are equal.

This property of parabolas has an important application in optics. The reflection of a light beam by a mirror is such that the incidence angle and the reflection angle, measured with respect to the normal to the mirror in the incidence point, are equal, that is the normal is the bisector of the angle formed by the two rays. By the demonstrated property, in the parabolic mirrors all the rays parallel to the axis of the mirror converge in its focus.

In the following JavaScript application the circle represents the source of a light beam (represented in yellow) parallel to the optical axis; the circle represents the focus; the red ray is perpendicular to the tangent at the point where the light beam strikes the parabolic mirror.