Bose Integrals

(edited by Roberto Bigoni)

The integrals of form

fig.1

which must be calculated, for example, in the black body theory, may be written

fig.2

The introduced sum indeed is a geometric series of common ratio e-x. If x>0 then 0<e-x<1 and, when the common ratio q is <1,

fig.3

Therefore

fig.4

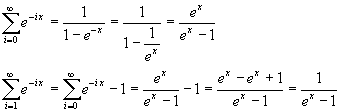
The integral of the sum is the sum of the integrals of its terms: then

fig.5

To calculate the integral fig.6 we can let t=ix; so

fig.7

The integral fig.8 is the function Γ(n+1) (Euler's Gamma) that, for natural positive integer, coincides with the factorial n!

fig.9

Now we can write

fig.10

By introducing the function ζ (Riemann's zeta) (limitedly to natural arguments)

fig.11

we finally have

fig.12

The values of ζ for natural even arguments were calculated by Euler. Here are the first of them

n ζ(n)
2 π2
‾‾‾
6
4 π4
‾‾‾
90
6 π6
‾‾‾‾‾
945
8 π8
‾‾‾‾‾‾
9450

Then the integrals In with odd n have the following values

n In
1 π2
‾‾‾
6
3 π4
‾‾‾
15
5 8π6
‾‾‾‾‾
63
7 8π8
‾‾‾‾‾‾
15

 

Last Revised: May 2018