10. The ζ (zeta) function

In the previous sections we have seen how, given a real function of real variable, one can find its series expansion about 0; it is inversely possible define a real function giving an infinite convergent sum. This is the way L. Euler used to define the ζ function for real variables. After him, B. Riemann extended the domain of this function to complex numbers. Now this function is known as the Riemann's ζ function. Here, however, we consider only real arguments.

The Riemann's ζ (zeta) function is defined as

If x=1, the (10.1) is the harmonic series, which don't converge. So for x=1 the function has a singularity.

The values of ζ(n), when n is an even natural number, can be exactly deduced. The method, found by L. Euler, may be the following.

• Starting from the MacLaurin series expansion of the sine

  

  when x≠0, one can get

  

  p(x) has the same zeroes of sin x, excluding 0.

• In general, a polynomial P(x), with non-null zeroes x_k and such that P(0)=1, may be factorized as

  

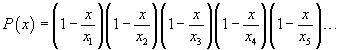
  Therefore p(x) may be written

  

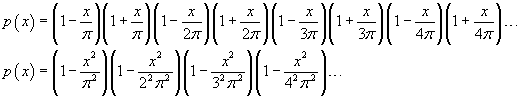
• To fast the calculation, let ; we get

  

  The MacLaurin series expansion of p(α) is

  

• The first derivative of p(α) may be calculated using the logarithmic derivative method

  

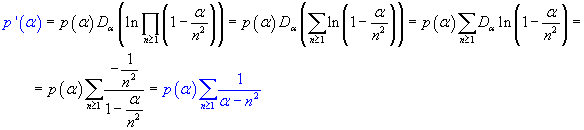
  For α=0 we get

  

  p'(0)α must coincide with , therefore

  

  Finally we get the value of ζ(2)

  

• From p'(α) we can have p''(α)

  

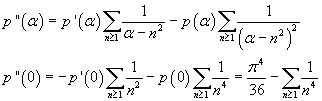
  must coincide with , so

  

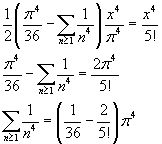
  From that we get the value of ζ(4)

  

• From p''(α) we can get p'''(α)

  

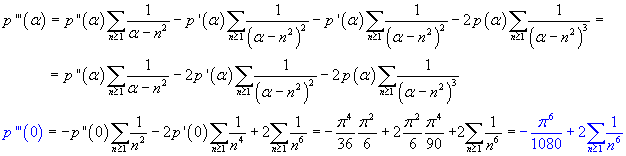
  must coincide with , therefore

  

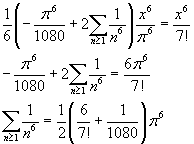
  Finally, the value of ζ(6) is

  

These values of ζ are strictly correlated with the Bernoulli's numbers; they are particular cases of a general relation true for all the natural even numbers:

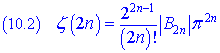
From this relation we have also

The extension of the domain of ζ to the real and complex number shows that also the integer negative arguments generate values related to the Bernoulli's numbers. It can be demonstrated that, for natural numbers n≥2,

that is

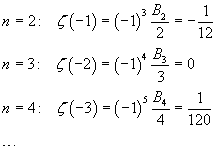
The Bernoulli's numbers with odd index ≥ 3 are all 0, so the values of ζ for negative even integer values are all 0.

For arguments other than 1, the values of ζ can be numerically approximated (P. Borwein in "An Efficient Algorithm for the Riemann Zeta Function").

The following JavaScript application allows you to approximate the values of Z for real arguments. If your browser does not allow the iframe tag, you can open the source page.