(notes by Roberto Bigoni)
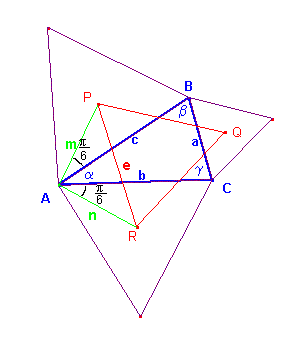
Click on the points A, B, C to move them, avoiding to alter their counterclockwise ordering .
In mathematical literature the following theorem is usually called Napoleon's Theorem.
If, on any side of a triangle, we construct three equilateral triangles outside the triangle and we join their centers, we get an equilateral triangle.
It may be a useful exercise to prove this theorem by using some well-known trigonometric identities.

With reference to the figure, we note first that m is two thirds the height of the equilateral triangle of side c and n is two thirds the height of the equilateral triangle of side b:
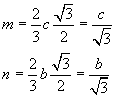
By applying the cosine theorem to the triangle APR we obtain
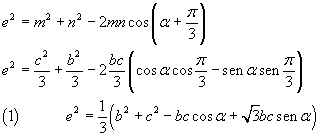
and by applying the cosine theorem to the triangle ABC we obtain
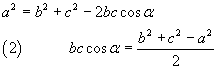
If we represent by S the area of the triangle ABC we have
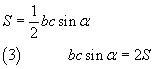
Using the identities (2) and (3), from (1) we obtain
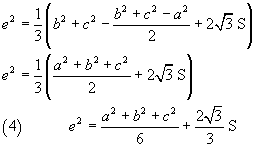
The identity (4) shows that, given the triangle ABC, the measure of the side PR, depends only on the measures of sides a, b, c of the triangle, ie it does not depends on the angle α. Similarly we can prove that this is also true for the sides RQ and QP, so they have the identical measure e. So the triangle PQR is equilateral.
last revised: January 29, 2016