The exponential, circular and hyperbolic functions, whether direct or inverse, like the real constants π and e, would be not much useful if we could not calculate their values.
However, it must be clear that, since they are real numbers, in general it isn't possible to thoroughly express these values, like we do with natural numbers. In general, to calculate a real number α means to find an algorithm which generates a sequence of rational numbers an converging to α. The more n increases, the more an approximates α. In the practical applications we use sufficiently good approximations.
Maybe the more simple example of such sequences is the sequence of the powers with natural exponent n of a rational number x such that |x|<1. The more n increases, the more the terms xn of this sequence approach 0. We may formally express this by saying that for all rational number x, such that |x|<1
![]()
(the limit of the sequence xn equals 0)
if and only if for every positive real number ε there is a natural
number nε such that
![]() for every n>nε.
for every n>nε.
This could be a good starting point to find other useful sequences converging the real numbers generated by the transcendental functions.
It can easily checked that, for every real number x,
![]()
and that, if x≠1,
![]()
The sum in (7.2) is a geometric series, because the sequence of its addends is a geometric sequence, that is the ratio of any two successive addends is constant.
The limit for n→∞ of the series equals the limit of the fraction:
![]()
If |x|<1, using a simplified notation,
![]()
From (7.3) we have also
![]()
Geometric series in WolframAlpha.
The fraction
![]() is the derivative with respect to x of ln(1+x).
is the derivative with respect to x of ln(1+x).
Hence, for |x|<1 and remembering that ln1=0,
we can vice versa say that ln(1+x) is the antiderivative
of the sum
![]() and therefore
and therefore
![]()
![]()
So it is possible to approximate the natural logarithm of the numbers in the interval ]0;2[ and the approximation will be better the more one increases the number of the addends in the sum.
The sum (7.5) is said Mercator's series. This series has a limited convergence domain and converges very slowly, but from it we can deduce other series converging over all the logarithm domain.
In fact, from the Mercator's series we have
![]()
Subtracting term by term the (7.6) from the (7.5) and remembering the basic properties of the logarithm we obtain
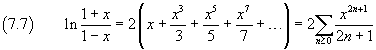
The (7.7) can be rewritten as
![]()
The first term in (7.8) equals the hyperbolic arctangent, so
![]()
From the (7.4) we can write
![]()
Integrating both the terms and remembering that arctan(0)=0, we have
![]()
From the (7.10), remembering that
![]() we obtain
an algorithm to approximate π
we obtain
an algorithm to approximate π
![]()
This way to approximate π is known as Leibniz's series.
Arctangent series expansions in WolframAlpha.
If we consider the Mercator's series (7.5), we could find that the coefficients cn of
the powers xn in the sum are such that ![]() ,
where f(n)(0) denotes the value of the n-th derivative of the function applied to 0 and n!
is the factorial of the index n.
To can apply the given expression of cn also when n=0, we assume that f(0)(x)
is the function itself and 0!=1.
,
where f(n)(0) denotes the value of the n-th derivative of the function applied to 0 and n!
is the factorial of the index n.
To can apply the given expression of cn also when n=0, we assume that f(0)(x)
is the function itself and 0!=1.
We could find the same thing for the arctangent functions (7.9) and (7.10) and, in general, for every other infinitely differentiable function f(x), if the function and its derivatives are calculable for x=0. In fact, from
![]()
we can get
So for every other infinitely differentiable function f(x), if the function and its derivatives are calculable for x=0, we have
![]()
the (7.13) is said MacLaurin's series expansion
The more immediate series expansion we can get using the (7.13) is that of the natural exponential ex for which all the derivatives coincide with the function itself which, when x=0, has value 1.
![]()
The series (7.14) allows to approximate the number e=e1
![]()
From the (7.14) we have also
![]()
From the (7.14), (7.16) and (3.9), we get the series for the hyperbolic cosine and sine, which could however be directly deduced from the (7.13)
![]()
![]()
Series expansions of the exponential and hyperbolic sine and cosine in WolframAlpha.
From the (7.13) we can easily deduce the series expansion of the circular cosine and sine
![]()
![]()
If we use the (7.17) to expand coshix, where i is the imaginary unit, we get
![]()
![]()
If we use the (7.18) to expand sinhix, we get
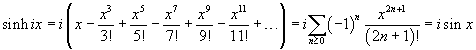
![]()
From the (7.21) and the (3.9) we get
![]()
From the (7.22) and the (3.9) we get
![]()
Gathering all together
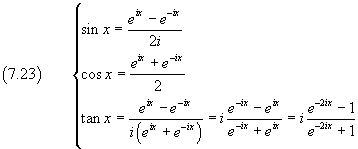
These are the well known and very important Euler's formulas.
From the (7.23) we have also
![]()
which allows to express a complex number z, with modulus ρ and argument θ, in both the following ways:
![]()
Series expansions of the circular sine and cosine in WolframAlpha.
Given the function
![]()
real for x<1, its successive derivatives are
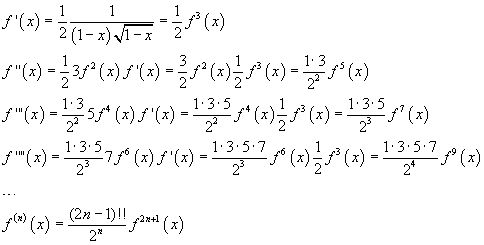
where the double exclamation mark next to the natural number n represents the double factorial of the number itself, that is
Since f(0)=1, the MacLaurin's series expansion of f(x) results
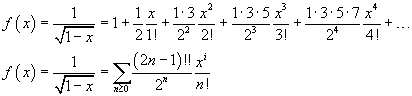
Moreover, for -1<x<1, we have
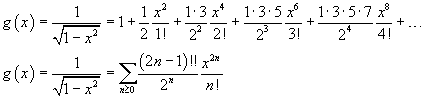
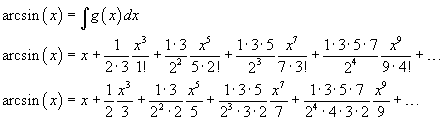
and , finally
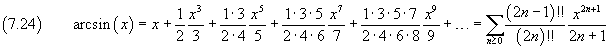
The cosine of an angle is equal to the sine of its complementary angle, therefore
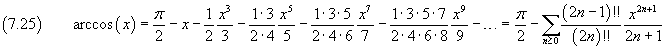
We can obtain the expansion (7.24) in a more direct way if we expand the function (7.23) using the generalized binomial coefficients. Infact from
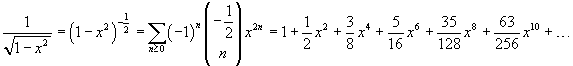
we have
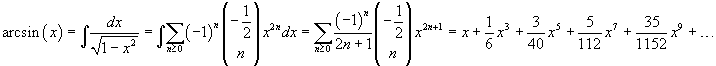
In a similar way we can get
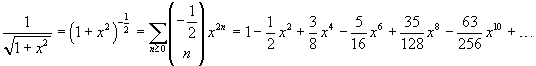
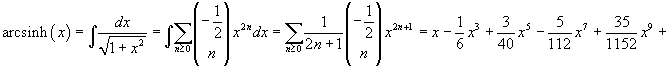
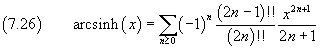
The hyperbolic arccosine is real only if its argument is ≥1. If, however, we want its MacLaurin series expansion, we can proceed as follows
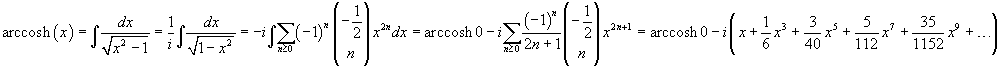
Furthermore we have
![]()
so
![]()
and finally
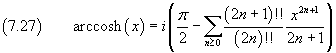
Series expansions with WolframAlpha.
Other very useful series expansions can be found in Fourier series expansion.