La legge di Planck

1. Il corpo nero.

Quando le onde elettromagnetiche colpiscono la superficie di un corpo, l'energia da esse trasportata, a seconda della loro frequenza e delle interazioni con gli atomi e le molecole del corpo da essa dipendenti,

o viene assorbita dal corpo stesso che, in generale, si scalda
o viene riflessa.

Se, ad esempio, un raggio di luce solare, che, come dimostrano gli spettri ottenibili con prismi o reticoli, comprende numerose frequenze, colpisce gli oggetti di un ambiente, le frequenze assorbite concorrono a riscaldare gli oggetti, quelle riflesse vengono captate dagli occhi e concorrono a formare il colore degli oggetti stessi.

Le superfici perfettamente assorbenti si scaldano molto ed appaiono nere. Quelle perfettamente non assorbenti non si scaldano e appaiono bianche.

La migliore realizzazione concettuale, oltre che pratica, di una superficie perfettamente nera, cioè perfettamente assorbente, detta anche corpo nero, è costituita da una piccola apertura in una cavità chiusa: la radiazione che penetra nell'apertura non può più uscire dalla cavità, quindi è completamente assorbita.

A loro volta atomi e molecole situati alla superficie dei corpi emettono radiazioni elettromagnetiche, quindi emettono energia. È comune osservare che i corpi caldi, come, ad esempio, i filamenti delle lampadine ad incandescenza, emettono luce.

Dato che le superfici molto calde, come appunto un filamento di lampadina o una stella, emettono molto molto di più di quanto non assorbano, esse si comportano con ottima approssimazione come superfici nere. Questo non implica, come testimoniato dalla comune esperienza, che esse appaiano nere. Quindi un corpo nero rispetto all'assorbimento non è affatto nero rispetto all'emissione.

L'energia emessa da una superficie nera è distribuita su onde di varia lunghezza λ e corrispondente frequenza ν. Si osserva sperimentalmente che la lunghezza d'onda λ_max per la quale si ha la massima emissione di corpo nero è inversamente proporzionale alla sua temperatura assoluta (legge dello spostamento di Wien - 1893)):

Ad esempio, osservando che il colore prevalente nella luce solare è il giallo, che corrisponde ad una lunghezza d'onda di circa 480 nanometri, si può stimare la temperatura della superficie del Sole:

La legge dello spostamento spiega perché le stelle più calde del sole appaiono blu, quelle più fredde appaiono rosse.

L'energia totale emessa da un'unità di superficie nell'unità di tempo, è detta irradianza R.

L'irradianza risulta sperimentalmente proporzionale alla quarta potenza della temperatura assoluta (legge di Stefan-Boltzmann - 1879).

L'irradianza massima si ha per il corpo nero, per cui risulta:

La costante di proporzionalità σ è nota come costante di Stefan-Boltzmann e vale

Assumendo che la temperatura della superficie del Sole sia di 6000K, ogni metro quadro di superficie solare emette ogni secondo 7,35·10⁷ J di energia.

2. La soluzione di Planck.

Plank, nel 1900, riuscì a determinare un'espressione analitica dell'irradianza in funzione della lunghezza d'onda capace di rendere conto sia della legge di Stefan sia delle legge di spostamento di Wien:

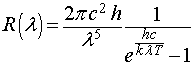
In questa espressione c è la velocità della luce, k è la costante di Boltzmann, h è una costante il cui valore dipende dal valore della costante di Stefan-Boltzmann. Integrando questa funzione di λ su tutti i valori possibili di λ, cioè da 0 a ∞ si ottiene

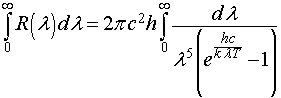
Per risolvere l'integrale conviene anzitutto operare un cambiamento di variabile

ottenendo

Si dimostra che

In definitiva

L'irradianza totale risulta quindi proporzionale alla quarta potenza della temperatura assoluta, come stabilito dalla legge di Stefan-Boltzmann. Uguagliando i coefficienti di T⁴ si può ottenere il valore di h:

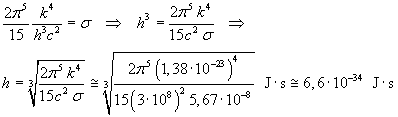
Usando metodi di misura più precisi, per il valore di h si ottiene h ≅ 6,6260693 · 10^-34 J·s. h è nota come costante di Planck.

Per verificare se la funzione R(λ) soddisfa anche alla legge dello spostamento, cioè per vedere a quale λ si ha il massimo di irradianza, si azzera la sua derivata prima. Per facilitare l'elaborazione conviene ricorrere alla stessa sostituzione di variabile usata per l'integrazione:

Si ottiene

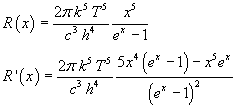
Azzerando questa espressione si ha

La soluzione esatta di questa equazione non è agevole, ma si può ottenere una buona approssimazione con un metodo numerico. Si ottiene x_max ≅ 4,96511 e quindi

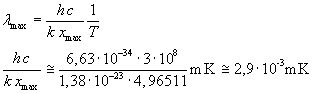
Si ottiene una costante di proporzionalità in ottimo accordo con la C della legge di spostamento di Wien.

3. L'analisi di Einstein e Bose.

La funzione trovata da Planck risultò quindi molto efficace, ma non risultava spiegabile con i principi della meccanica, termodinamica ed elettromagnetismo classici. Una sua coerente deduzione si deve al lavoro congiunto di Einstein e del fisico indiano Satyendra Nath Bose (1924).

Si ipotizza che le onde elettromagnetiche in una cavità chiusa siano onde stazionarie con nodi sulle pareti, cioè che si comportino come le onde meccaniche su una corda tesa con estremi fissi. Ovviamente l'analisi, rispetto al modello della corda tesa, va generalizzata considerando la tridimensionalità delle onde e.m.

Considerando per semplicità una cavità cubica di spigolo l, il versore della velocità dell'onda è individuato dai coseni degli angoli che esso forma con una terna di spigoli concorrenti nello stesso vertice. Questi coseni sono noti come coseni direttori.
Detti α, β γ questi tre angoli, le uniche onde stazionarie possibili sono quelle per cui

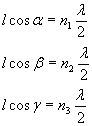
Elevando al quadrato entrambi i membri di queste uguaglianze, poi sommandole membro a membro e ricordando che, per definizione, la somma dei quadrati dei coseni direttori è 1, si ottiene

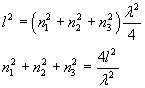
Ricordando poi che λ ν = c si ha

Ogni terna (n₁, n₂, n₃) individua una possibile onda stazionaria nella cavità.

Interpretando n₁, n₂ e n₃ come coordinate in uno spazio tridimensionale, nonostante queste coordinate debbano essere numeri naturali, se l è sufficientemente grande, esse possono essere pensate come variabili continue e l'equazione ottenuta può essere interpretata come quella di una sfera di raggio e il numero Z di tutte le frequenze minori o uguali a ν è dato da un ottavo del volume di tale sfera:

Ma, tenendo conto del fatto che le onde e.m. sono onde trasversali con due stati ortogonali di polarizzazione, questo numero va raddoppiato. Inoltre l³ è il volume V della cavità:

Le onde stazionarie possono assumere solo frequenze discrete, individuate, come s'è detto, dalla terna di valori discreti (n₁, n₂, n₃) e ad ognuna di esse è associata una certa dose finita di energia.

Seguendo l'impostazione data al problema da Einstein e Bose, si possono quindi interpretare queste onde anche come particelle distinte, dette fotoni: ogni fotone contiene un quanto di energia ε = hν ed è individuato dalla terna (n₁, n₂, n₃): questi sono i suoi numeri quantici.

Nella cavità c'è un gas di fotoni. Questi fotoni però non possono però essere completamente assimilati alle particelle della meccanica classica, in quanto, dal modo con cui vengono concepiti, non è possibile stabilire esattamente la loro posizione. L'unica informazione sensata sulla loro posizione è che è situata nel volume V della cavità.

Ma c'è un'altra differenza molto importante rispetto ai gas di particelle classiche analizzati nei lavori di Boltzmann e Maxwell: anche se praticamente è impossibile farlo, concettualmente le particelle classiche si possono contare. Si può dire, ad esempio, che una mole di un gas contiene un numero ben preciso di molecole, cioè il numero di Avogadro. I fotoni sono continuamente emessi ed assorbiti dalle pareti: non si possono contare nemmeno concettualmente.

L'analisi statistica di un gas di fotoni deve quindi essere inevitabilmente diversa dall'analisi condotta da Boltzmann sui gas di particelle materiali. Questa analisi è nota come statistica di Bose-Einstein.

La densità ζ di fotoni, cioè il numero di fotoni per unità di volume, risulta

Il numero n di possibili valori distinti della loro energia h ν per unità di volume per frequenze comprese tra ν e (ν+dν) può essere ottenuto dal differenziale di questa espressione:

Ognuna delle n energie può essere posseduta da m fotoni; m è detto numero di occupazione. Il numero w delle possibili combinazioni di n elementi a gruppi di m risulta pertanto

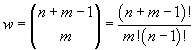
Questo è vero per ognuno degli intervalli di ampiezza hν in cui può essere suddiviso lo spettro delle energie, cioè di ognuno dei livelli energetici. Indicando con n_i e m_i i parametri relativi ad ognuno di questi livelli si ha che il numero totale di possibili distribuzioni di fotoni è dato da

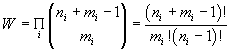
Se il un gas di fotoni è in equilibrio la distribuzione più stabile è quella che massimizza il valore di W e quindi anche del suo logaritmo.

Calcolando il logaritmo di W e usando le approssimazioni di Stirling, si ottiene

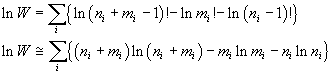
Indicando con ε_i l'energia associata ad ogni frequenza, deve essere

Con questo vincolo, si può calcolare il massimo del logaritmo di W con il metodo dei moltiplicatori di Lagrange:

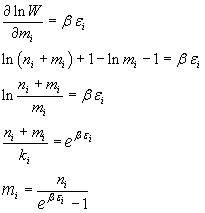
Le considerazioni termodinamiche sviluppate da Boltzmann dimostrano che

Quindi, ponendo ε = h ν, si ha che il valore del numero di occupazione m per una cavità in equilibrio termico è

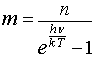
Ognuno degli m fotoni ha energia h ν, i livelli energetici per unità di volume sono , dunque l'energia per unità di volume, cioè la densità di energia risulta

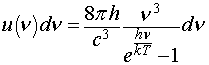
La stessa densità di energia in funzione si λ risulta

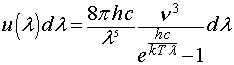
Questa relazione equivale a quella determinata da Planck.

Si consideri una superficie sferica di raggio r. La radiazione emessa dalla superficie, propagandosi a velocità c, riempie uno strato di spessore dr in un tempo .

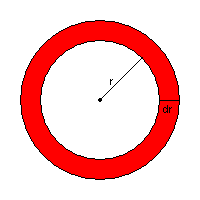
Ogni elemento dS di superficie irraggia energia in tutte le direzioni. Rappresentando l'intensità dell'energia emessa in una particolare direzione con un vettore di lunghezza dr, il contributo di ognuno di questi vettori all'energia totale è dato dalla componente radiale di questo vettore.

Scelto un sistema di riferimento cartesiano ortogonale con origine O in dS, asse x radiale, assi y e z tangenti alla superficie in O, indicando con β l'angolo che il vettore forma con l'asse y e con α l'angolo che la proiezione del vettore sul piano xz forma con l'asse x,

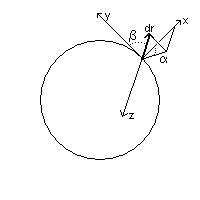
la componente radiale vale . Integrando su tutta la superficie sferica e su tutti i valori degli angoli α e β si ottiene l'energia totale dU presente nello strato di spessore dr.

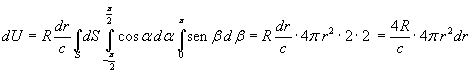
dU si ottiene anche moltiplicando la densità u(λ) per il volume dV dello strato, che si ottiene dal differenziale del volume della sfera:

Uguagliando le due espressioni di dU si ottiene

4. La nascita della meccanica quantistica.

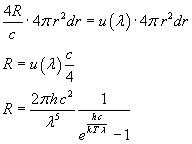
Il lavoro di Bose e Einstein dimostrò che per spiegare la funzione di Planck bisognava ricorrere ad idee completamente nuove nell'analisi della radiazione elettromagnetica:

l'emissione e l'assorbimento di energia elettromagnetica di frequenza ν da parte di atomi e molecole non avviene in modo continuo, ma per dosi discrete multiple di hν;
conseguentemente l'energia di atomi e molecole non può variare in modo continuo, ma solo per multipli di hν;
viceversa, atomi e molecole emettono energia elettromagnetica in quantità discrete ΔU alle quali e associata una frequenza
la propagazione dell'energia, che nella meccanica classica è descritta da onde, può anche essere modellizzata con un flusso di particelle;
se di queste particelle è nota l'energia, esse non sono localizzabili al di sotto di una certa soglia di determinazione.

Tutte queste congetture nel corso degli anni 20 del XX secolo sono state fortemente corroborate dagli studi teorici e sperimentali di numerosi fenomeni, di cui si ricordano i principali:

la teoria di Einstein dell'effetto fotoelettrico;
la teoria dei calori specifici molari di Debye;
la teoria degli spettri atomici di Bohr-Sommerfeld;
l'effetto Compton;
la dinamica della relatività ristretta;

Lo studio di questi fenomeni e di quelli simmetrici relativi alla meccanica delle particelle subatomiche, in particolare degli elettroni (De Broglie), portò la comunità mondiale dei fisici alla definizione sempre più completa e organica della Meccanica Quantistica, una teoria completamente nuova dei fenomeni atomici e subatomici e dei campi elettromagnetici, con una profonda revisione delle teorie di Newton e di Maxwell che fino ad allora avevano dominato gli studi fisici.

ultimo aggiornamento:Maggio 2018