Integrali di Bose

Gli integrali del tipo

fig.1

che si incontrano, ad esempio, nella teoria del teoria del corpo nero possono essere scritti anche nel seguente modo

fig.2

Infatti la sommatoria introdotta è una serie geometrica di ragione e^-x; per x>0 si ha che 0<e^-x<1 e per una nota proprietà delle serie geometriche di ragione q<1

Applicando questa proprietà si ha

fig.4

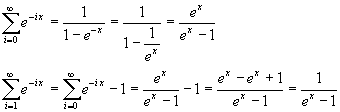
L'integrale di una somma è uguale alla somma degli integrali degli addendi: dunque

fig.5

Il calcolo dell'integrale fig.6 può essere reso più agevole introducendo la variabile t=ix; si ottiene

fig.7

L'integrale fig.8 è la funzione Γ(n+1) (Gamma di Eulero) che, per argomenti naturali, coincide con il fattoriale n!

fig.9

Ora si può scrivere

Introducendo la funzione ζ (zeta) di Riemann (limitatamente ad argomenti naturali)

si ottiene infine

I valori di ζ per argomenti naturali pari sono stati calcolati da Eulero. Si ha

n	ζ(n)
2	π² ‾‾‾ 6
4	π⁴ ‾‾‾ 90
6	π⁶ ‾‾‾‾‾ 945
8	π⁸ ‾‾‾‾‾‾ 9450

Per gli integrali I_n con n dispari si ha quindi

n	I_n
1	π² ‾‾‾ 6
3	π⁴ ‾‾‾ 15
5	8π⁶ ‾‾‾‾‾ 63
7	8π⁸ ‾‾‾‾‾‾ 15

ultima revisione: Maggio 2018