Appunti per i Licei
(da Note Didattiche)
Nel piano cartesiano xOy, se a2+b2+4c>0, un'equazione di forma
![]()
rappresenta una circonferenza di centro C
![]()
e raggio
![]()
Poiché nella (1) compaiono tre parametri (a, b, c), sono sufficienti tre condizioni indipendenti per determinare completamente l'equazione della circonferenza.
In particolare, dati tre punti non allineati P, Q, R:
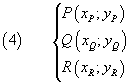
l'equazione della circonferenza per i tre punti può essere determinata imponendo che le coordinate dei tre punti soddisfino l'equazione (1), cioè risolvendo il sistema
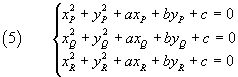
È possibile risolvere il problema anche in altri modi, ad esempio calcolando le equazioni degli assi dei segmenti PQ e QR e le coordinate α e β del punto C in cui gli assi si intersecano: C è il centro della circonferenza. Si calcola poi la distanza di C da uno dei tre punti e si ottiene il raggio ρ. L'equazione della circonferenza è data da
![]()
Sviluppando i quadrati dei binomi nella (6) si ottiene
![]()
Poiché la (7) deve coincidere con la (1), tra i parametri a, b, c e i parametri α, β e ρ devono valere le seguenti identità
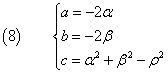
La seguente applicazione Javascript automatizza la soluzione del problema. Quando le coordinate dei punti sono razionali (cioè non contengono il punto di separazione decimale ma possono contenere la barra di frazione) anche i parametri a, b e c sono espressi da numeri razionali.
L'applicazione, oltre a calcolare equazione, centro e raggio, produce il grafico della circonferenza.
Per attivare l'applicazione il vostro browser deve permettere l'uso di Javascript e permettere i popup.
ultima revisione: 19/09/2018