Appunti per i Licei Scientifici
(da Note Didattiche)
Dati in un piano una retta d e un punto F esterno a d e distante f da d, si dice conica l'insieme dei punti P del piano tali che, detta H la loro proiezione ortogonale su d, il rapporto PF/PH abbia valore costante e (e>0).
![]()
La retta d è detta direttrice della conica e il punto F è detto fuoco della conica.
Il rapporto e è detto eccentricità della conica.
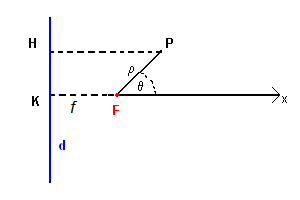
Per descrivere analiticamente una conica di eccentricità e e parametro f si può scegliere
un sistema di riferimento polare con polo in F e semiasse polare dato dalla semiretta con origine in F,
perpendicolare a d e orientata verso la parte opposta a d.
La retta contenente il semiasse polare è detta asse polare.
In tale sistema ad ogni punto P del piano è associata biunivocamente una coppia di numeri reali (ρ;θ),
detti rispettivamente modulo e anomalia di P, tali che
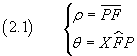
dove X rappresenta un punto della semiretta polare KF successivo ad F e l'angolo θ è orientato in senso antiorario, misurato in radianti e compreso nel primo giro.
In questo sistema di riferimento la (1.1) diventa
![]()
da cui
![]()
e, indicando il prodotto ef con l,
![]()
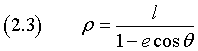
Il parametro l è detto semilato retto della conica.
La (2.3) è l'equazione polare di una conica di semilato retto l ed eccentricità e.
Poiché il coseno è una funzione pari, cioè assume lo stesso valore per argomenti opposti, la (2.3) esplicita una importante caratteristica di tutte le coniche: sono simmetriche rispetto all'asse polare.
Dalla (2.3) si deduce che, quando θ è un angolo retto, ρ coincide con l;
questa osservazione permette di interpretare geometricamente il parametro l:
l coincide con la distanza dal fuoco dei due punti della conica di anomalie rispettivamente
![]() .
.
Dalla (2.3) si deduce inoltre che 1-e cosθ deve essere positivo
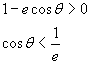
Nell'ultimo caso, le semirette dal polo ai punti di anomalie
![]() sono dette asintoti della conica.
sono dette asintoti della conica.
Volendo ottenere l'equazione della conica in coordinate cartesiane, si può scegliere come sistema di riferimento un sistema xFy con origine nel fuoco F, con l'asse delle ascisse coincidente con l'asse polare e con l'asse delle ordinate perpendicolare all'asse polare per F.
In tale sistema di riferimento si ha
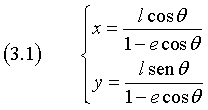
Dalla prima delle (3.1) si ricava
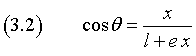
e, elevando al quadrato entrambi i membri della (3.1),
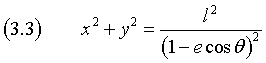
Sostituendo la (3.2) nella (3.3) ed eseguendo le naturali semplificazioni si ottiene
![]()
Va notato che la (3.4), ottenuta elevando al quadrato entrambi i membri della (3.1), è suvvalente a quest'ultima e quindi il luogo descritto dalla (3.1) è un sottinsieme del luogo descritto dalla (3.4). Usualmente la denominazione di conica si estende ai luoghi descritti dalla (3.4).
La (3.4) può essere scritta
![]()
Si dimostra che, se P(xP,yP) è un punto della conica, allora l'equazione della retta tangente alla conica nel punto P è
![]()
cioè l'equazione della tangente può essere ricavata direttamente da quella della conica:
Se l'eccentricità e è nulla, la (2.3) diventa semplicemente
![]()
cioè la conica è il luogo dei punti di modulo costante, vale a dire il luogo dei punti che hanno ugual distanza dal polo F. La conica è quindi la circonferenza di centro F e raggio l.
Volendo ottenere l'equazione della circonferenza in coordinate cartesiane ortogonali, ponendo e=0 nella (3.4) si ottiene
![]()
Se si assume un sistema di riferimento cartesiano un sistema XΩY, con assi paralleli a quelli del sistema sopra indicato e con origine in Ω(-α;-β), le relazioni tra le coordinate dei due sistemi sono espresse da
![]()
Nel nuovo sistema di riferimento le coordinate del centro sono α e β e la (5.2) diventa
![]()
In generale, ogni equazione di forma equivalente alla (5.3) è l'equazione cartesiana di una circonferenza con centro C(α;β) e raggio l.
Indicando con x e y le variabili, la (5.3) diventa
![]()
Sviluppando i quadrati dei binomi si ottiene
![]()
![]()
Introducendo i parametri
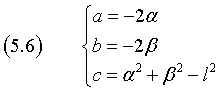
la (5.5) assume forma
![]()
Le equazioni di questa forma rappresentano quindi una circonferenza con centro C(α;β)
![]()
e raggio r
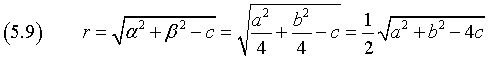
Se il radicando a2+b2-4c non è positivo, la circonferenza non è reale.
Se l'eccentricità e è uguale a 1, la conica è il luogo dei punti equidistanti da fuoco e direttrice e, usando una nomenclatura introdotta da Apollonio di Perga, è detta parabola.
In questo caso l coincide con f e la (2.3) diventa
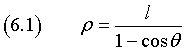
Poiché il denominatore del secondo membro non si può annullare, è immediato dedurre che una parabola non ha punti di anomalia nulla e che quando l'anomalia di un punto della parabola tende a 0 o a 2π la distanza del punto dal fuoco tende all'infinito.
La distanza di un punto dal fuoco è minima quando θ è uguale a π, caso in cui
tale distanza è la metà di f.
Il punto V più vicino al fuoco è detto vertice della parabola e si trova sull'asse polare nel punto medio del segmento FK.
L'equazione della parabola in coordinate cartesiane ortogonali nel sistema xFy si ottiene immediatamente dalla (3.4) con e=1:
![]()
Se si assoggetta la (6.2) alla traslazione
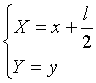
che sposta l'origine del sistema di riferimento da F a V, si ottiene
![]()
Esprimendo x in funzione di y
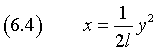
In generale si potrà dire che ogni equazione
![]()
rappresenta una parabola simmetrica rispetto all'asse delle ascisse con vertice nell'origine e fuoco e direttrice dati da
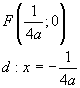
Confrontando la (6.4) con la (6.5) si ha
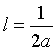
Questa identità permette di ottenere immediatamente la (6.5) in coordinate polari.
Se, come si è fatto per la circonferenza, si assume un sistema di riferimento cartesiano un sistema XΩY, con assi paralleli a quelli del sistema sopra indicato e con origine in Ω(-α;-β), le relazioni tra le coordinate dei due sistemi sono espresse da
![]()
Nel nuovo sistema di riferimento le coordinate del vertice sono α e β e la (6.5) diventa
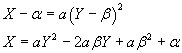
Viceversa, ogni equazione di forma
![]()
rappresenta l'equazione di una parabola con asse di simmetria parallelo all'asse delle ascisse e vertice V(α ; β) tale che
![]()
cioè
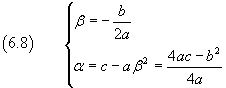
Analogamente, ogni equazione
![]()
rappresenta una parabola simmetrica rispetto all'asse delle ordinate con vertice nell'origine e fuoco e direttrice dati da
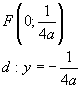
e ogni equazione di forma
![]()
rappresenta l'equazione di una parabola con asse di simmetria parallelo all'asse delle delle ordinate e vertice V(α ; β) tale che
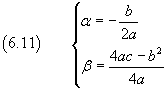
Approfondimento: Area del segmento parabolico
Approfondimento: Proprietà ottica del fuoco
Se l'eccentricità e della conica è compresa tra 0 e 1, la conica è detta ellisse.
In questo caso il denominatore della (2.3) è sempre positivo e tutti i punti dell'ellisse hanno distanza finita dal fuoco.
In particolare: il punto V' con distanza minima dal è quello di anomalia θ=π che dista dal fuoco
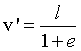
Il punto V'' di distanza massima è quello di anomalia θ=0 che dista dal fuoco
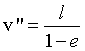
Questi due punti sono detti vertici dell'ellisse e sono ovviamente situati sull'asse polare su cui è situato anche F.
Nel sistema xFy le ascisse dei vertici si ottengono ponendo y=0 nell'equazione (3.4)
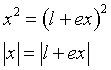
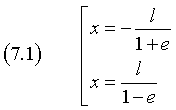
Il segmento V''V' è detto asse focale dell'ellisse e la sua misura risulta
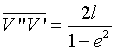
Indicando con a la misura del semiasse focale, si ha
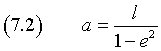
Un'equazione cartesiana dell'ellisse alternativa rispetto alla (3.4) può essere ottenuta scegliendo come origine O il punto medio del segmento V"V', mantenendo come asse delle ascisse l'asse polare e come asse delle ordinate la perpendicolare all'asse delle ascisse per l'origine. Questo sistema di riferimento è detto sistema canonico.
L'ascissa del punto medio di V''V' è
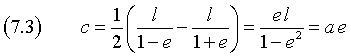
da cui
![]()
e quindi, usando la (7.4), dalla (7.2) si ottiene
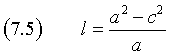
La traslazione nel nuovo sistema di riferimento è
![]()
Traslando la (3.4) si ottiene
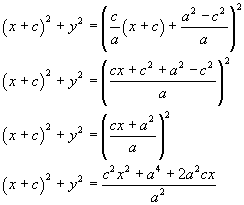
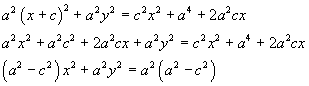
Ponendo
![]()
si ha
![]()
e infine
![]()
La (7.7) è detta equazione canonica dell'ellisse.
Dato che l'equazione della curva dipende solo dai quadrati delle variabili essa risulta simmetrica sia rispetto all'asse delle ascisse sia rispetto all'asse delle ordinate sia rispetto all'origine. Per x=0 si ha y = ± b. Il parametro b rappresenta quindi la misura del semiasse minore.
La simmetria della curva implica che, oltre al fuoco usato come polo nella (2.3), di ascissa -c, la curva ammette un altro fuoco ad esso simmetrico di ascissa +c.
L'equazione (7.6) implica a>b. Nel caso che in un'equazione di forma (7.7) si abbia a<b, l'equazione rappresenta un'ellisse in cui l'asse focale coincide con l'asse delle ordinate e le distanze |c| dei fuochi dall'origine, centro dell'ellisse, sono date da
![]()
Con la posizione (7.6) la (7.5) diventa
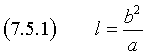
Questa identità, assieme alla (7.4), permette di ottenere immediatamente la (7.7) in coordinate polari.
Si dimostra che per qualunque punto dell'ellisse la somma delle sue distanze dai fuochi è uguale alla misura dell'asse maggiore, cioè 2a.
Se si assume un sistema di riferimento con origine in Ω(-α;-β) e assi paralleli ed equiversi a quelli del sistema canonico l'equazione dell'ellisse diventa
![]()
Se l'eccentricità e della conica è maggiore di 1, la conica è detta iperbole.
Poiché ρ è intrinsecamente positivo anche il denominatore della (2.3) deve essere positivo: quindi sono ammissibili solo punti per i quali
![]()
cioè
![]()
Quando θ si avvicina agli estremi di questo intervallo la distanza ρ del punto dal fuoco tende all'infinito, quindi le iperboli, come le parabole e a differenza delle circonferenze e delle ellissi, sono curve che non si chiudono.
Il punto V' di distanza minima è quello di anomalia θ=π che dista dal fuoco
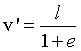
Questo punto è detto vertice dell'iperbole ed è ovviamente situato sull'asse polare su cui è situato anche F.
Tuttavia la (3.4), che è suvvalente alla (2.3), per y=0, fornisce le ascisse (7.1) che, per evidenziare che, con e>1, sono entrambe negative e per esplicitare il loro ordinamento, si riscrivono
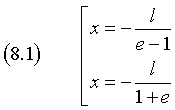
Denominando V'' il punto di ascissa minore (vertice secondario), il segmento V''V' è detto asse reale dell'iperbole e la sua misura risulta
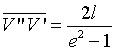
Indicando con a la metà di questa distanza si ha
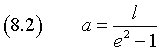
Come si è fatto per l'ellisse, una equazione per l'iperbole alternativa alla (3.4) può essere ottenuta traslando l'origine
del sistema di riferimento da F a O, punto medio dell'asse reale.
L'ascissa di tale punto medio, nel sistema xFy, è
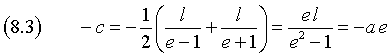
e quindi
![]()
Usando la (8.4) dalla (8.2) si ottiene
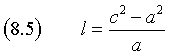
La traslazione nel nuovo sistema di riferimento è
![]()
Traslando la (3.4) si ottiene
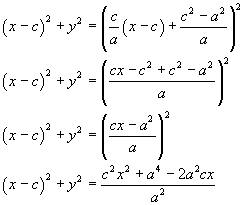
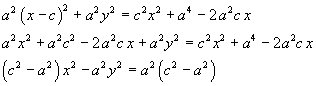
Ponendo
![]()
si ha
![]()
e infine
![]()
La (8.7) è detta equazione canonica dell'iperbole.
Questa equazione è più generale della (2.3) perché è stata ottenuta uguagliando due
espressioni del quadrato del modulo ρ. Dato che l'equazione della curva dipende solo dai
quadrati delle variabili essa risulta simmetrica sia rispetto all'asse delle ascisse sia
rispetto all'asse delle ordinate sia rispetto all'origine.
La simmetria della curva implica che, oltre al fuoco usato come polo, di ascissa c,
la curva ammette un altro fuoco ad esso simmetrico di ascissa -c.
Scrivendo la (8.6) nella seguente forma
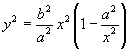
si osserva che la curva non ammette punti reali nella regione (-a<x<a). La curva è formata da due rami separati.
Si osserva inoltre che per x di valore assoluto crescente la curva tende ad assimilarsi alla coppia di rette
![]()
passanti per l'origine e di coefficienti angolari
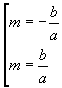
dette asintoti dell'iperbole
L'equazione (8.7) implica che l'asse reale dell'iperbole coincide con l'asse delle ascisse. Equazioni di forma
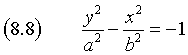
rappresentano iperboli con fuochi sull'asse delle ordinate.
Con la posizione (8.6) la (8.5) diventa
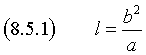
Questa identità, assieme alla (8.4), permette di ottenere immediatamente la (8.7) in coordinate polari.
Si dimostra che per qualunque punto dell'iperbole il modulo della differenza delle sue distanze dai fuochi è uguale alla misura dell'asse maggiore, cioè 2a.
Area del segmento iperbolico retto
Costruzione dell'iperbole dati i semiassi a e b
Dati nel piano cartesiano Oxy la direttrice d di equazione
![]()
e il fuoco Φ(xΦ,yΦ), l'insieme dei punti P(x,y) appartenente alla conica di eccentricità e, per la (1.1) è espresso dall'equazione
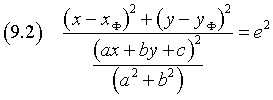
Nella (9.1) i parametri a, b, c sono definiti a meno di un fattore di proporzionalità e a e b non possono essere entrambi nulli, quindi, senza perdita di generalità, nella (9.2) si può assumere
![]() ottenendo
ottenendo
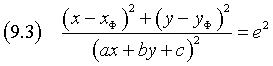
Sviluppando e semplificando
![]()
![]()
![]()
Quindi un'equazione di forma
![]()
in cui i parametri A, B, C, D, E, F sono definiti a meno di una costante di proporzionalità k (k≠0), può rappresentare un conica con
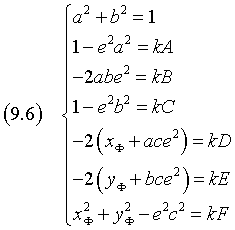
Si osserva che
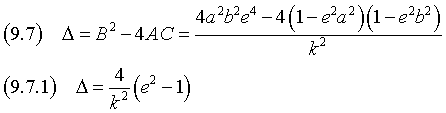
Quindi:
Esempio 1.
![]()
Δ = 0: è l'equazione di una parabola, quindi e = 1.
L'equazione è simmetrica rispetto alla bisettrice del primo quadrante; il fuoco si trova sull'asse di simmetria, quindi xΦ=yΦ.
La direttrice è perpendicolare all'asse di simmetria, quindi a=b.
Dalla (9.6) si ha
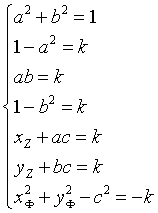
Dalla prima equazione si ha a2=1/2; b2=1/2
Dalla terza k=1/2;
Dalla quinta si ha
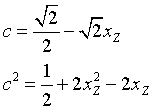
e, infine, dalla settima, xΦ=0 e c2=1/2. Quindi
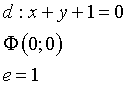
Esempio 2.
![]()
Δ < 0: è l'equazione di un'ellisse.
L'equazione è simmetrica rispetto alla bisettrice del primo quadrante; il fuoco si trova sull'asse di simmetria, quindi xΦ=yΦ.
La direttrice è perpendicolare all'asse di simmetria, quindi a=b.
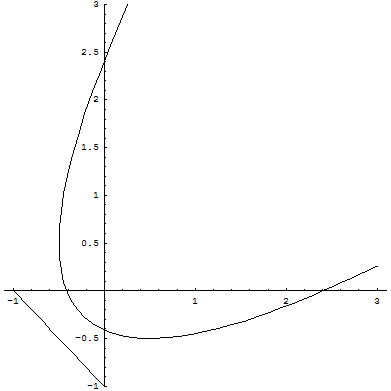
Dalla (9.6), assumendo e≠0 perché è presente un monomio in xy,
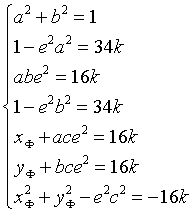
Dalla prima equazione si ha a2=1/2; b2=1/2
dalla terza
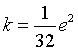
Dalla seconda si ha
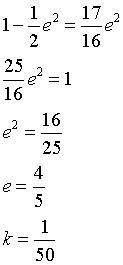
Dalla quinta si ha
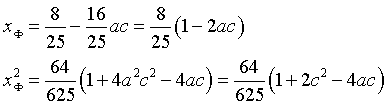
Dalla settima
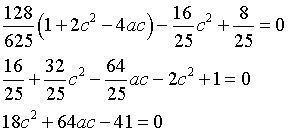
Per 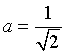 si ha
si ha
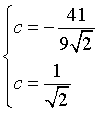
Per 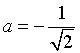
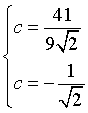
Le soluzioni sono equivalenti. In definitiva
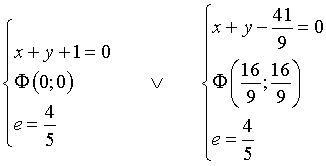

Equazione generale di una conica
ultima revisione: Gennaio 2022