Appunti per i Licei Scientifici
(da Note Didattiche)
Nel piano cartesiano xOy un'equazione di forma
![]()
può rappresentare una conica.
Poiché i coefficienti A, B, C, D, E, F della (1) sono definiti a meno di un fattore di proporzionalità, per determinarli saranno sufficienti cinque condizioni indipendenti che possono essere le coordinate di cinque punti P, Q, R, S, T tali che
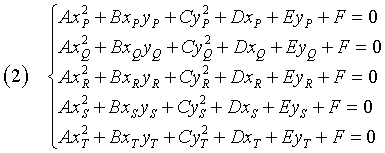
Per avere coefficienti determinati si può integrare il sistema con una condizione di normalizzazione arbitraria che imponga che l'equazione sia di 2° grado: ad esempio A + B + C = 1.
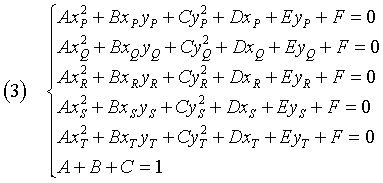
La seguente applicazione Javascript automatizza la soluzione del problema.
Quando tutte le coordinate dei punti sono razionali
(cioè non contengono il punto di separazione decimale e possono contenere la barra di frazione) anche i coefficienti A, B, C, D, E, F, sono espressi da numeri razionali esatti.
Le coordinate possono essere espresse anche in punto fisso o mobile o come espressioni (es. 1.2+1/4) o come valori di funzione (es. Sqrt[2], Sin[1]).
In questo caso i coefficienti sono approssimati da numeri reali con la parte decimale arrotondata al numero di cifre indicate nel campo decimali.
ultima revisione: Luglio 2018