Appunti per i Licei Scientifici
(da Note Didattiche)
Nel piano cartesiano xOy un'equazione di forma
![]()
può rappresentare un'ellisse con assi paralleli agli assi cartesiani con centro C(α;β) e semiassi a e b.
I denominatori nella (1) sono intrinsecamente positivi. Per semplificare la notazione e il calcolo conviene indicarli con i parametri positivi
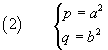
e riscrivere l'equazione nel seguente modo
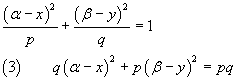
Poiché nella (3) compaiono quattro parametri (p, q, α, β ), sono sufficienti quattro condizioni indipendenti per determinare completamente l'equazione dell'ellisse.
In particolare, dati quattro punti non allineati P, Q, R, S:
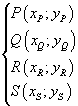
l'equazione dell'ellisse per i quattro punti può essere determinata imponendo che le loro coordinate soddisfino l'equazione (3), cioè risolvendo il sistema
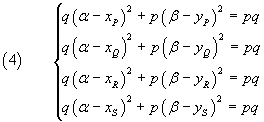
La risoluzione del sistema può essere resa più agevole se si osserva che sottraendo membro a membro la seconda equazione dalla prima si ha
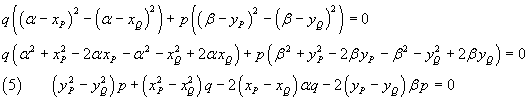
Per ottenere un'equazione lineare, nella (5) si pone
![]()
quindi
![]()
La stessa procedura può essere applicata a qualunque altra coppia di equazioni del sistema (4), ottenendo, ad esempio,
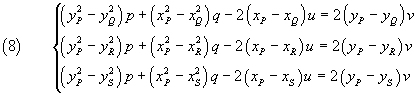
Il sistema (8) permette di esprimere p, q, u, e, conseguentemente, anche α e β, in funzione di v. Sostituendo queste espressioni in una qualunque delle equazioni del sistema (4), se il sistema è possibile, si possono determinare v e quindi i valori di p, q, α e β.
La seguente applicazione Javascript automatizza la soluzione del problema.
Quando le coordinate dei punti sono razionali (cioè non contengono il punto di separazione decimale ma possono contenere la barra di frazione) anche i parametri a, b, α e β, nei limiti delle possibilità di Javascript, sono espressi da numeri razionali, Se non è possibile, sono approssimati da numeri reali.
L'applicazione, oltre a calcolare equazione, centro e e semiassi, produce il grafico dell'ellisse.
ultima revisione: 10/04/2018