Appunti per i Licei Scientifici
(da Note Didattiche)
Nel piano cartesiano xOy, equazioni del tipo
![]()
con a≠0, rappresentano parabole con asse di simmetria parallelo all'asse delle ordinate, ed equazioni del tipo
![]()
rappresentano parabole con asse di simmetria parallelo all'asse delle ascisse.
Poiché nelle (1) e (2) compaiono tre parametri, sono sufficienti tre condizioni indipendenti per determinare l'equazione della parabola dell'uno o dell'altro tipo.
In particolare, dati tre punti A, B, C tali che i segmenti AB e BC non siano paralleli agli assi:
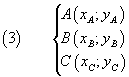
l'equazione della parabola che li comprende si ottiene imponendo che le coordinate dei punti soddisfino l'equazione della parabola. Per parabole di tipo (1) si ha
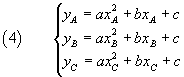
e per parabole di tipo (2)
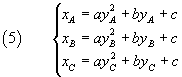
La seguente applicazione Javascript automatizza la soluzione del problema. Quando le coordinate dei punti sono razionali (cioè non contengono il punto di separazione decimale ma possono contenere la barra di frazione) anche i parametri a, b e c sono espressi da numeri razionali.
L'applicazione calcola l'equazione, il vertice e il fuoco e produce il grafico della parabola nella zona adiacente al fuoco.
La massima distanza dal fuoco va espressa nel campo di input max. ρ.
Per attivare l'applicazione il vostro browser deve permettere l'uso di Javascript e permettere i popup.
ultima revisione: 19/09/2018