Appunti per i Licei Scientifici
(a cura di Roberto Bigoni)
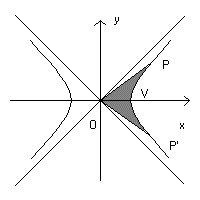
Dall'equazione canonica dell'iperbole è immediato dedurre le espressioni delle coordinate di un punto P dell'iperbole nel primo quadrante in funzione di una variabile comune rappresentata dall'area α delimitata dal segmento OP (dove O è l'origine del sistema canonico), dal segmento OP' (con P' simmetrico di P rispetto all'asse delle ascisse) e l'arco di iperbole PP'. Se il punto P è nel quarto quadrante, α si assume negativo.

Infatti, posto
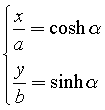
elevando al quadrato entrambi i membri e sommando membro a membro si ottiene l'equazione canonica
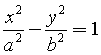
Esprimendo x e y in funzione di α
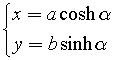
si ottengono le equazioni parametriche dell'iperbole.
Variando il parametro α da -∞ a +∞ si ottengono le coordinate dei punti del ramo di iperbole nel primo e quarto quadrante. Il ramo nel secondo e terzo quadrante è il suo simmetrico.
ultima revisione: 10/06/2016