Appunti per i Licei Scientifici
(a cura di Roberto Bigoni)

Data la parabola di equazione
![]() e la retta di equazione
e la retta di equazione
![]() , sia
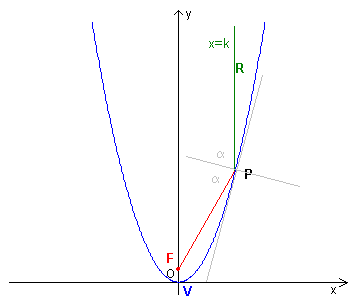
F il fuoco della parabola, P il punto comune alle due curve, R un punto della retta
tale che, se a>0, abbia ordinata maggiore di quella di P, altrimenti minore.
, sia
F il fuoco della parabola, P il punto comune alle due curve, R un punto della retta
tale che, se a>0, abbia ordinata maggiore di quella di P, altrimenti minore.
Si dimostra che la bisettrice dell'angolo convesso FPR coincide con la normale alla parabola nel punto P. (La normale ad una curva in un punto è la perpendicolare alla tangente alla curva nello stesso punto.)
Le coordinate del fuoco sono
![]() e quelle di P sono
e quelle di P sono
![]() ,
dunque l'equazione della retta FP è
,
dunque l'equazione della retta FP è
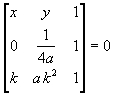
Sviluppando il determinante si ottiene
![]()
Le equazioni delle bisettrici degli angoli formati dalle rette FP e FR sono
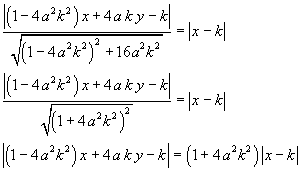
Passando dai valori assoluti ai valori relativi
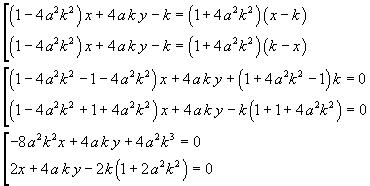
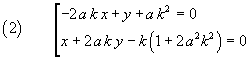
Come ci si deve attendere, le due bisettrici risultano perpendicolari in quanto i loro coefficienti angolari sono antireciproci.
Per la regola di sdoppiamento la tangente alla parabola nel suo punto P è
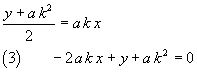
La (3) coincide con la prima delle (2), quindi una delle bisettrici coincide con la tangente e l'altra con la normale. Quindi gli angoli che le rette FP e RP formano con la normale alla parabola nel punto P sono uguali.
Questa proprietà delle parabole risulta importante in ottica: la riflessione dei raggi luminosi negli specchi è tale che raggi incidenti e raggi riflessi formano angoli uguali rispetto alla normale allo specchio nel punto di incidenza. Per la proprietà geometrica delle parabole ora dimostrata, negli specchi parabolici tutti i raggi paralleli all'asse dello specchio convergono nel suo fuoco.
Nella seguente applicazione Javascript il cerchietto
![]() rappresenta la sorgente di un raggio luminoso (rappresentato in giallo) parallelo all'asse ottico;
il cerchietto
rappresenta la sorgente di un raggio luminoso (rappresentato in giallo) parallelo all'asse ottico;
il cerchietto
![]() rappresenta il fuoco;
la semiretta rossa è la perpendicolare alla tangente nel punto in cui il raggio lumonoso incide sullo specchio parabolico.
rappresenta il fuoco;
la semiretta rossa è la perpendicolare alla tangente nel punto in cui il raggio lumonoso incide sullo specchio parabolico.
ultimo aggiornamento: 08/06/2016