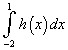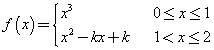Ministero dell'Istruzione, dell'Università e della Ricerca
M557 - ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE
Indirizzi: LI02, EA02 - SCIENTIFICO
LI03, EA09 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE

(Testo valevole anche per la corrispondente sperimentazione quadriennale)

 

Tema di MATEMATICA

 

Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario.

PROBLEMA 1

 

Il piano tariffario proposto da un operatore telefonico prevede, per le telefonate all'estero, un canone fisso di 10 euro al mese, più 10 centesimi per ogni minuto di conversazione. Indicando con x i minuti di conversazione effettuati in un mese, con f(x) la spesa totale nel mese e con g(x) il costo medio al minuto:
  1. individua l'espressione analitica delle funzioni f(x) e g(x) e rappresentale graficamente; verifica che la funzione g(x) non ha massimi né minimi relativi e dai la tua interpretazione dell'andamento delle due funzioni alla luce della situazione concreta che esse rappresentano.

  2. Detto x0 il numero di minuti di conversazione già effettuati nel mese corrente, determina x1 tale che

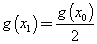
    Eqn001.gif

    Traccia il grafico della funzione che esprime x1 in funzione di x0 e discuti il suo andamento. Che significato ha il suo asintoto verticale?

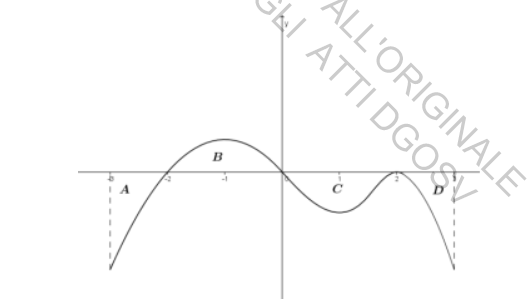
Sul suo sito web l'operatore telefonico ha pubblicato la mappa che rappresenta la copertura del segnale telefonico nella zona di tuo interesse:

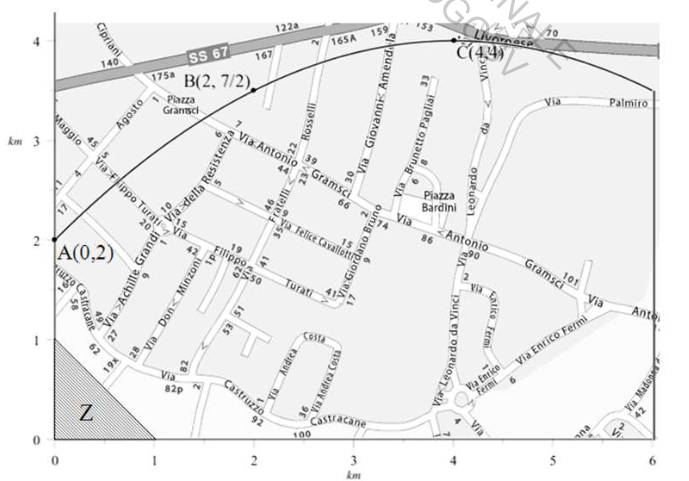
fig01.png

La zona è delimitata dalla curva passante per i punti A, B e C, dagli assi x e y e dalla retta di equazione x = 6; la porzione etichettata con la "Z" rappresenta un'area non coperta dal segnale telefonico dell'operatore in questione.

  1. Rappresenta il margine superiore della zona con una funzione polinomiale di secondo grado, verificando che il suo grafico passi per i tre punti A, B e C. Sul sito web dell'operatore compare la seguente affermazione:" nella zona rappresentata dalla mappa risulta coperto dal segnale il 96% del territorio"; verifica se effettivamente è così.

L'operatore di telefonia modifica il piano tariffario, inserendo un sovrapprezzo di 10 centesimi per ogni minuto di conversazione successivo ai primi 500 minuti.

  1. Determina come cambiano. di conseguenza, le caratteristiche delle funzioni f(x) e g(x), riguardo agli asintoti, alla monotonia, continuità e derivabilità, individua eventuali massimi e minimi assoluti della funzione g(x) e della sua derivata e spiegane il significato nella situazione concreta.

svolgimento

 

PROBLEMA 2

La funzione derivabile y = f(x) ha, per x ∈ [-3,3], il grafico Γ. disegnato in figura 2. Γ presenta tangenti orizzontali per x = -1, x = 1, x = 2. Le aree delle regioni A, B, C e D sono rispettivamente 2, 3, 3 e 1. Sia g(x) una primitiva di f(x) tale che g(3) = -5.

fig02.png

  1. Nel caso f(x) fosse esprimibile con un polinomio, quale potrebbe essere il suo grado minimo? Illustra il ragionamento seguito.
  2. Individua i valori di x ∈ [-3,3] per cui g(x) ha un massimo relativo e determina i valori xi x per i quali g(x) volge la concavità verso l'alto.
  3. Calcola g(0) e, se esiste, il Eqn002.gif
  4. Sia Eqn003.gif; determina il valore di Eqn004.gif

svolgimento

 

QUESTIONARIO

 

  1. Determinare l'espressione analitica della funzione y = f(x) sapendo che la retta Eqn005.gif è tangente al grafico di f nel secondo quadrante e che Eqn006.gif

    svolgimento

  2. Dimostrare che il volume del tronco di cono è espresso dalla formula

    Eqn007.gif

    dove R ed r sono i raggi e h l'altezza.

    svolgimento

  3. Lanciando una moneta sei volte qual è la probabilità che si ottenga testa "al più" due volte? Qual è la probabilità che si ottenga testa "almeno" due volte?

    svolgimento

  4. Di quale delle seguenti equazioni differenziali la funzione Eqn008.gif è soluzione?

    svolgimento

  5. Determinare un'espressione analitica della retta perpendicolare nell'origine al piano di equazione Eqn013.gif

    svolgimento

  6. Sia f la funzione, definita per tutti gli x reali, da

    Eqn014.gif

    determinare il minimo di f.

    svolgimento

  7. Detta A(n) l'area del poligono regolare di n lati inscritto in un cerchio C di raggio r, verificare che Eqn015.gif e calcolarne il limite per n→∞

    svolgimento

  8. I lati di un triangolo misurano, rispettivamente, 6 cm, 6 cm e 5 cm. Preso a caso un punto P all'interno del triangolo, qual è la probabilità che Pdisti più di 2 cm da tutti e tre i vertici del triangolo?

    svolgimento

  9. Data la funzione:

    Eqn016.gif

    determinare il parametro k in modo che nell'intervallo [0,2] sia applicabile il teorema di Lagrange e trovare il punto di cui la tesi del teorema assicura l'esistenza.

    svolgimento

  10. Il grafico della funzione Eqn017.gif divide in due porzioni il rettangolo ABCD avente vertici Eqn018.gif. Calcolare il rapporto tra le aree delle due porzioni.

    svolgimento

_______________________________________________________________

Durata massima della prova: 6 ore.
È consentito l’uso della calcolatrice non programmabile.
È consentito l’uso del dizionario bilingue (italiano-lingua del paese di provenienza) per i candidati di madrelingua non italiana.
Non è consentito lasciare l’Istituto prima che siano trascorse 3 ore dalla dettatura del tema.