Ministero dell'istruzione e del merito

A002 - ESAME DI STATO CONCLUSIVO DEL SECONDO CICLO DI ISTRUZIONE
Testo valevole per tutti i seguenti indirizzi:
LI02, LI03, LI15, LI1S, LI22, LI23, LI31, LI32, LIA2, LIAO,
LIB2, LIC2, LID2, LII2, LII3, LII4, LIIS, LIS2, EA02, EA10
Disciplina: MATEMATICA

Il candidato risolva uno dei due problemi e risponda a 4 quesiti del questionario.

PROBLEMA 1

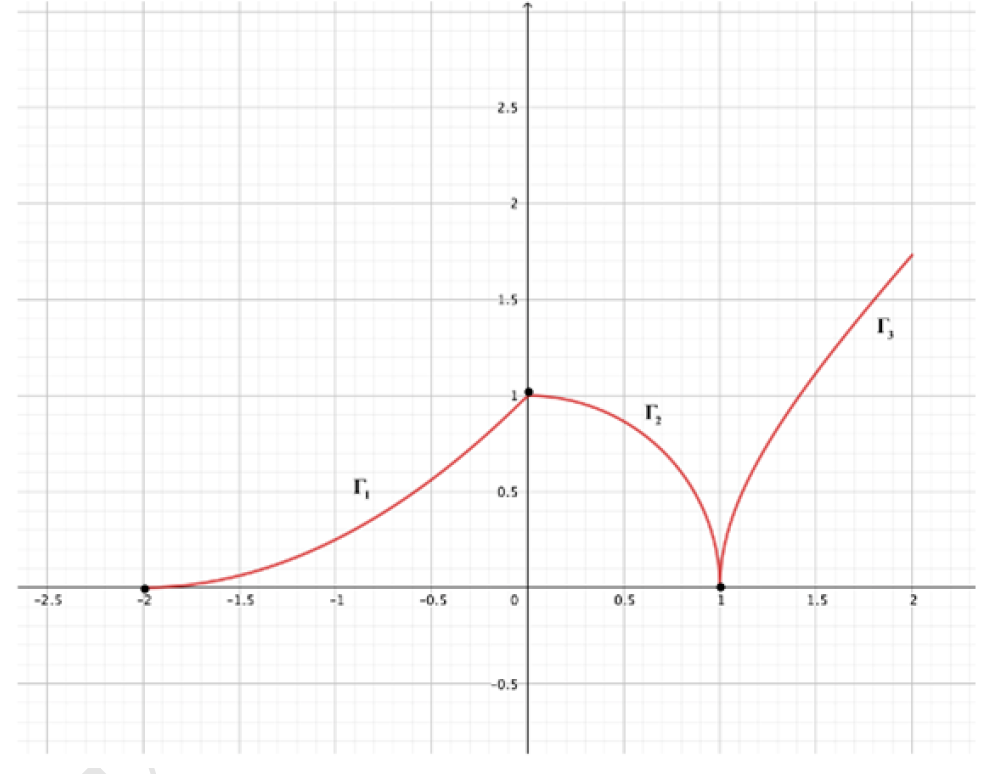
Il grafico in figura, rappresentativo della funzione continua 𝑦=𝑓(𝑥), è unione dell’arco di parabola Γ₁, dell’arco di circonferenza Γ₂ e dell’arco di iperbole Γ₃.

1. Scrivere un’espressione analitica della funzione 𝑓 definita a tratti nell’intervallo [−2;2], utilizzando le equazioni:

         

   e individuare i valori opportuni per i parametri reali a, b, c.

   Studiare la derivabilità della funzione 𝑓 e scrivere le equazioni delle eventuali rette tangenti nei punti di ascissa

   𝑥=−2     𝑥=0   𝑥=1     𝑥=2.

2. A partire dal grafico della funzione 𝑓, dedurre quello della sua derivata 𝑓′ e individuare gli intervalli di concavità e convessità di .
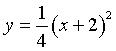3. Si consideri la funzione , definita nell’intervallo [−2;0], di cui Γ₁ è il grafico rappresentativo. Spiegare perché essa è invertibile e scrivere l’espressione analitica della sua funzione inversa ℎ. Studiare la derivabilità di ℎ e tracciarne il grafico.
4. Sia 𝑆 la regione limitata del secondo quadrante, compresa tra il grafico Γ₁ e gli assi cartesiani. Determinare il valore del parametro reale k affinché la retta di equazione x=k divida S in due regioni equivalenti.

svolgimento

PROBLEMA 2

Fissato un parametro reale a, con a≠0, si consideri la funzione f_a così definita:

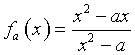
il cui grafico sarà indicato con .

1. Al variare del parametro a, determinare il dominio di f_a, studiarne le eventuali discontinuità e scrivere le equazioni di tutti i suoi asintoti.
2. Mostrare che, per 𝑎≠1, tutti i grafici Ω_a intersecano il proprio asintoto orizzontale in uno stesso punto e condividono la stessa retta tangente nell’origine.
3. Al variare di 𝑎<1, individuare gli intervalli di monotonia della funzione f_a. Studiare la funzione e tracciarne il grafico Ω_-1.
4. Determinare l’area della regione limitata compresa tra il grafico Ω_-1, la retta ad esso tangente nell’origine e la retta .

svolgimento

QUESITI

1. Sia ABC un triangolo rettangolo in A. Sia O il centro del quadrato BCDE costruito sull’ipotenusa, dalla parte opposta al vertice A.
   Dimostrare che O è equidistante dalle rette AB e AC.

   svolgimento

2. Un dado truccato, con le facce numerate da 1 a 6, gode della proprietà di avere ciascuna faccia pari che si presenta con probabilità doppia rispetto a ciascuna faccia dispari. Calcolare le probabilità di ottenere, lanciando una volta il dado, rispettivamente:
   - un numero primo
   - un numero almeno pari a 3
   - un numero al più pari a 3
   

   svolgimento

3. Considerata la retta 𝑟 passante per i due punti 𝐴(1,−2,0) e 𝐵(2,3,−1), determinare l’equazione cartesiana della superficie sferica di centro 𝐶(1,−6,7) e tangente a 𝑟.

   svolgimento

4. Tra tutti i parallelepipedi a base quadrata di volume 𝑉, stabilire se quello di area totale minima ha anche diagonale di lunghezza minima.

   svolgimento

5. Determinare l’equazione della retta tangente alla curva di equazione nel suo punto di ascissa 3, utilizzando due metodi diversi.

   svolgimento

6. Determinare i valori dei parametri reali a e b affinché:

   

   svolgimento

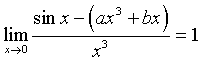
7. Si consideri la funzione:

   

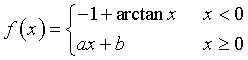
   Determinare per quali valori dei parametri reali a, b la funzione è derivabile. Stabilire se esiste un intervallo di ℝ in cui la funzione 𝑓 soddisfa le ipotesi del teorema di Rolle. Motivare la risposta.

   svolgimento

8. Data la funzione , definita nell’insieme dei numeri reali, stabilire per quali valori del parametro 𝑎>0 la funzione possiede tre zeri reali distinti.

   svolgimento

_______________________________________________________________

Durata massima della prova: 6 ore.
È consentito l’uso di calcolatrici scientifiche e/o grafiche purché non siano dotate di capacità di calcolo simbolico. (Nota MIM n. 9305 del 20 marzo 2023).
È consentito l’uso del dizionario bilingue (italiano-lingua del paese di provenienza) per i candidati di madrelingua non italiana.
Non è consentito lasciare l’Istituto prima che siano trascorse 3 ore dalla consegna della traccia.