Ministero dell'istruzione e del merito

A002 - ESAME DI STATO CONCLUSIVO DEL SECONDO CICLO DI ISTRUZIONE
Testo valevole per tutti i seguenti indirizzi:
LI02, LI03, LI15, LI1S, LI22, LI23, LI31, LI32, LIA2, LIAO,
LIB2, LIC2, LID2, LII2, LII3, LII4, LIIS, LIS2, EA02, EA10
Disciplina: MATEMATICA

Il candidato risolva uno dei due problemi e risponda a 4 quesiti del questionario.

PROBLEMA 1

Si consideri 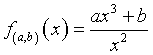, con .

a) Determinare i valori dei parametri in modo che la retta t, di equazione , sia tangente al grafico di nel suo punto P di ascissa .

Si ponga, d'ora in avanti, a=1 e b=4.

b) Studiare la funzione 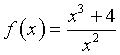e tracciarne il grafico γ. Scrivere l'equazione dell'ulteriore retta tangente alla curva γ passante per P.

c) Al variare del parametro reale m, determinare il numero di intersezioni tra la retta di equazione e la curva γ.

d) Sia , con 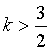, l'area della regione finita di piano compresa tra la curva γ, il suo asintoto obliquo, la retta t e la retta di equazione . Calcolare il , fornendo un'interpretazione geometrica del risultato ottenuto.

svolgimento

PROBLEMA 2

«All'inizio e alla fine, abbiamo il mistero. [...] A questo mistero la matematica ci avvicina, pur senza penetrarlo». (E. De Giorgi).

Si consideri la famiglia di funzioni , con e .

a)
Verificare che, qualunque sia il valore di n, la funzione f_n non è derivabile nel punto di ascissa x=0.
Determinare il valore di n in corrispondenza del quale il grafico di f_n presenta un punto angoloso.
Per opportuni valori dei parametri a, b, il grafico α, in figura, rappresenta la funzione .
Determinare i parametri a e b, considerando che f₂ è definita in [-1;1] e che il suo grafico è simmetrico rispetto all'asse delle ordinate.

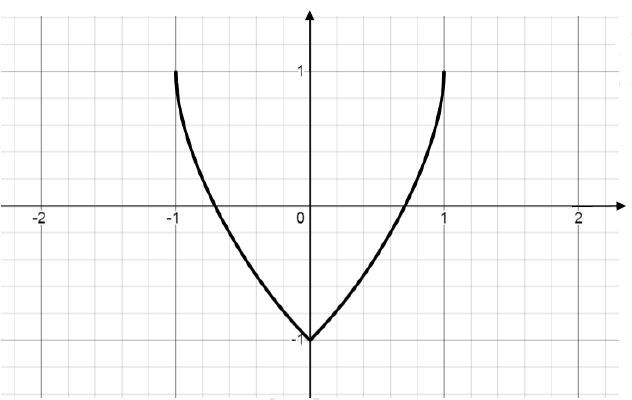
Si ponga, d'ora in avanti, a=-1, b=0.

b)
Studiare la funzione , verificando che non è derivabile negli estremi del dominio e nel punto di ascissa x=0.
Indicare con β il suo grafico e tracciare la curva .

c)
La retta r, di equazione x=k, con -1<x<1, interseca γ nei punti P e Q.
Dimostrare che la misura del segmento PQ è massima quando r è asse di simmetria di γ.

d)
Verificare che la funzione 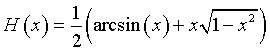è una primitiva della funzione .
Con il metodo che si ritiene più opportuno, calcolare l'area della regione finita di piano delimitata da γ.

«Le forme create dal matematico, come quelle create dal pittore o dal poeta, devono essere belle: le idee, come i colori o le parole, devono legarsi armoniosamente. La bellezza è il requisito fondamentale: al mondo non c'è posto perenne per la matematica brutta» (G. H. Hardy)

svolgimento

QUESITI

1. È dato un triangolo abc, rettangolo in B. Dimostrare che tale triangolo è isoscele se e solo se l'altezza BH relativa all'ipotenusa è congruente a metà ipotenusa.

   svolgimento

2. Si lancia 5 volte una moneta truccata che dà testa con probabilità p.
   - Qual è la probabilità di ottenere testa esattamente 2 volte?
   - Per quale valore di p la probabilità di ottenere testa esattamente 2 volte è massima?

   svolgimento

3. Nello spazio con riferimento cartesiano ortogonale Oxyz, è dato il piano .
   - Determinare le coordinate del punto H, proiezione ortogonale di P(4,2,1) sul piano π;
   - Determinare l'intersezione della retta 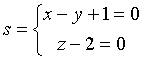con il piano π.

   svolgimento

4. Dimostrare che l'equazione ammette un'unica soluzione positiva.

   svolgimento

5. Determinare la funzione polinomiale di quarto grado y=p(x) sapendo che, in un sistema di riferimento cartesiano, il suo grafico verifica le seguenti condizioni:
   - è tangente all'asse x nell'origine;
   - passa per il punto (1,0);
   - ha un punto stazionario in (2,-2).

   svolgimento

6. Si consideri la funzione integrale
   
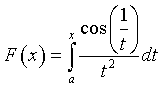
   con x≥a, in cui a indica un parametro reale positivo. Determinare il più grande valore di a in modo che .

   svolgimento

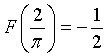7. Il prossimo 5 luglio la terra raggiungerà l'afelio, il punto della propria orbita in cui è massima la distanza dal Sole, pari a circa 1,52·10¹¹ m.
   Il perielio è invece il punto che si trova alla minima distanza dal Sole, pari a circa 1,47·10¹¹ m.
   Determinare, in un opportuno sistema di riferimento, l'equazione che rappresenta la traiettoria della Terra intorno al Sole.

   svolgimento

8. Scrive Carlo Emilio Gadda in uno dei racconti de L'Adalgisa - Disegni milanesi: «Le stanze del servizio, il bagno, i corridoi, l'anticamera e l'uno de' due gabinetti, eran pavimentati con piastrelle rosse di piccolo formato: esagonali [...]. L'apotèma di quelle mattonelle misurava centimetri 5,196: mentreché il raggio del circolo circoscritto raggiungeva i 60 millimetri».
   Esprimere la relazione esatta tra raggio del cerchio circoscritto ed apotema (ossia il raggio del cerchio inscritto) per un esagono regolare. Verificare il risultato ottenuto alla luce delle misure indicate dallo scrittore. Spiegare perché, utilizzando piastrelle esagonali regolari tutte congruenti, è possibile pavimentare un piano. Con quali altri poligoni regolari, tra loro congruenti, è possibile pavimentare un piano?
   Motivare la risposta.

   svolgimento

Durata massima della prova: 6 ore.
È consentito l'uso di calcolatrici scientifiche o grafiche purché non siano dotate della capacità di elaborazione simbolica algebrica e non abbiano la disponibilità di connessione a Internet.
È consentito l'uso del dizionario bilingue (italiano-lingua del paese di provenienza) per i candidati di madrelingua non italiana. Non è consentito lasciare l'Istituto prima che siano trascorse 3 ore dalla consegna della traccia.