Problema 1

testo della prova

Quesito 1

Ponendo si ottiene

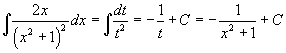
Dalla condizione al contorno si ha C=0 quindi

Quesito 2

Risolvendo la disequazione 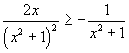si ha

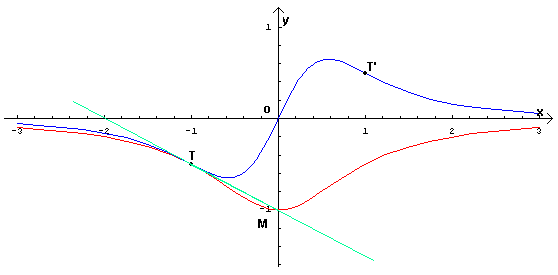
L'uguaglianza si ha solo per x=-1. Il punti comune alle due curve è .

La derivata di F(x) è f(x), quindi

La derivata di f(x) è

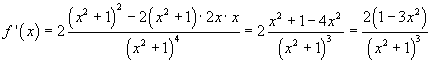
Quindi . Le due curve nel punto comune T hanno uguale coefficiente angolare: dunque sono tangenti.

L'equazione della retta tangente τ è

Quesito 3

Analisi di F(x)

• F(x) è reale per ogni x reale, è pari, ed è sempre negativa.
• Interseca l'asse delle ordinate nel punto M(0;-1); per x→±∞ tende a 0; ha un asintoto orizzontale nell'asse delle ascisse.

• La derivata prima di F(x) è f(x)

  

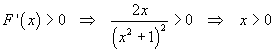
  F(x) cala in ]-∞;0[, cresce in ]0;+∞[, ha un minimo assoluto in M

• La derivata seconda di F(x) è f'(x)

  

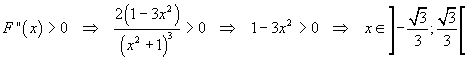
  F(x) ha concavità positiva in 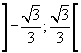, negativa in 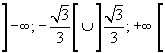e flessi obliqui nei punti di coordinate

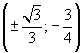
Analisi di f(x)

• f(x) è reale per ogni x reale, è dispari, è positiva per x positive, negativa per x negative. φ interseca gli assi nell'origine.
• Per x→±∞, f(x)→0: φ ha un asintoto orizzontale nell'asse delle ascisse.

• f(x) cresce in 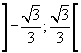, cala in 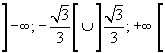e ha estremi nei punti di coordinate

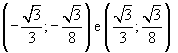
• La derivata seconda di f(x) è

  

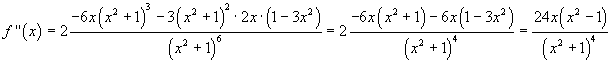
  e risulta positiva in

  

  γ ha concavità positiva in , negativa in e flessi obliqui nei punti di coordinate .

Quesito 4

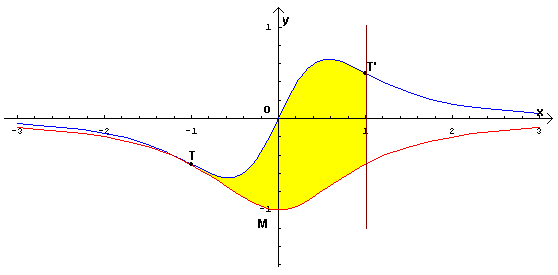
L'area richiesta è quella colorata in giallo nella figura. Si ottiene calcolando l'integrale .

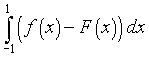Si ottiene

Quesito 5

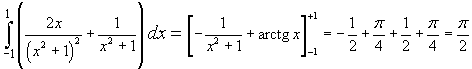
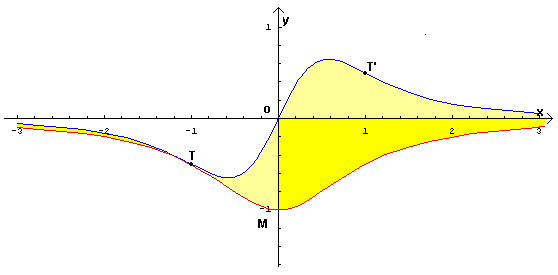
Le aree richieste possono essere ottenute calcolando i due integrali

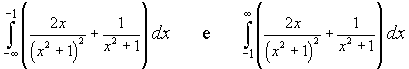
Si ha

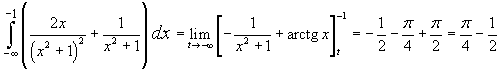
e

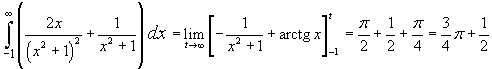
La somma delle due aree calcolate è π come ci si deve aspettare, dato che, per simmetria, è equivalente all'area compresa tra il diagramma della funzione e l'asse delle ascisse (vedere anche quesito 10).