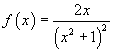Preparazione all'esame scritto di Matematica - 2006

Liceo Scientifico - P.N.I.

Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario.

Tema 1

Date le funzioni reali di variabile reale 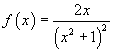e con :

1. dimostrare che l'equazione esplicita di F(x) è ;
2. dimostrare che e che nell'unico punto T in cui assumono lo stesso valore le due curve φ e Φ rappresentate dalle funzioni sono tangenti l'una all'altra; calcolare l'equazione della retta τ tangente ad entrambe.
3. disegnare nello stesso piano cartesiano Oxy φ e Φ;
4. calcolare l'area della parte di piano delimitata da φ, da Φ e dalla retta di equazione .
5. calcolare le aree delle parti di piano delimitate dai due diagrammi φ e Φ.

Svolgimento

Tema 2

Nel piano cartesiano Oxy le equazioni parametriche della curva γ sono

1. Dimostrare che l'equazione esplicita in coordinate cartesiane della curva γ è per i punti del primo e terzo quadrante, per i punti del secondo e quarto quadrante.
2. Sfruttando le simmetrie della y(x), disegnare la curva γ nella sua interezza.
3. Calcolare l'area circoscritta da γ.
4. Calcolare il volume del solido Γ generato dalla rotazione di γ attorno all'asse delle ascisse.
5. Determinare l'equazione di γ in coordinate polari.

Svolgimento

Quesiti

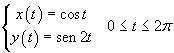
1. Verificare graficamente che l'equazione ammette un'unica soluzione compresa nell'intervallo e approssimare questa soluzione a meno di un centesimo usando il metodo delle tangenti.

Svolgimento

2. Calcolare il volume del solido generato dalla rotazione di un triangolo con lati di misure 2u, 3u e 4u attorno alla retta passante per il lato di lunghezza maggiore.

Svolgimento

3. La cima dello Stromboli, vista da un certo punto sulla superficie del mare, appare sottesa da un angolo di 5°17'46" rispetto alla riva dell'isola. Avvicinandosi di 5km all'isola, l'angolo tra la cima e la riva misura 10°30'12". Valutare l'altezza del vulcano.

Svolgimento

4. La funzione coseno iperbolico può essere espressa tramite l'esponenziale in base naturale come . Dopo aver spiegato perché tale funzione non è invertibile in tutto il suo dominio, individuarne un dominio di invertibilità ed esprimere la funzione inversa, valida in tale dominio, tramite la funzione inversa dell'esponenziale naturale.

Svolgimento

5. Proporre un algoritmo che approssimi il valore di π ed implementare tale algoritmo in un linguaggio di programmazione.

Svolgimento

6. Un punto si muove su una traiettoria piana con una velocità variabile nel tempo espressa dal vettore . Sapendo che nell'istante la posizione del punto è , calcolare la posizione del punto nell'istante . (tutte le misure si intendono espresse in unità S.I.)

Svolgimento

7. Nella circonferenza di diametro AB = 2r si tracci la corda MN perpendicolare ad AB e si conduca per il punto A, perpendicolarmente al piano della stessa circonferenza, il segmento AP = a. Posto , determinare il massimo volume della piramide PAMN.

Svolgimento

8. Stabilire per quali valori di a e b la funzione 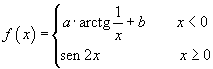risulta continua e derivabile nell'origine.

Svolgimento

9. Utilizzando un metodo di integrazione numerica, valutare l'integrale

Svolgimento

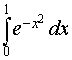
10. Qual è il raggio della circonferenza di area uguale a quella della parte di piano compresa tra il grafico della curva di equazione e l'asse della ascisse?

Svolgimento

• Problemi 1 2

• Quesiti 1 2 3 4 5 6 7 8 9 10