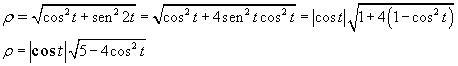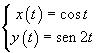si ottieneLa curva descritta dalle equazioni parametriche date è una delle note figure di Lissajou prodotte dalla composizione di due moti armonici.
Da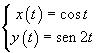
si ottiene
e,
se cos t non è nullo,
.
Dove x e y sono concordi in segno, cioè nel primo e terzo quadrante,
si ha
;
dove sono discordi, cioè nel secondo e quarto quadrante, si ha
Se cos t è nullo, è nullo pure sen 2t; in questo caso
le funzioni parametriche individuano l'origine O del piano cartesiano e le due espressioni
della y(x) sono continue in tutto il dominio
.
La y1 e la y2 sono entrambe dispari e quindi le curve da esse descritte sono simmetriche rispetto all'origine; inoltre la y2 e l'opposta della y1, quindi il suo diagramma è simmetrico di quello della y1 rispetto all'asse delle ordinate. Tutto il grafico di γ può essere quindi dedotto dal suo ramo situato nel primo quadrante. Basta quindi studiare l'andamento della y1 per x compreso tra 0 e 1.
In tale intervallo la y1 è non negativa e si annulla nei punti di ascissa 0 e 1.
La sua derivata prima è
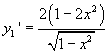e non
esiste per x=1. Nel punto
la curva
ha tangente verticale.
La derivata prima è positiva in
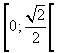e
negativa in
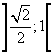, quindi
la funzione cresce nel primo intervallo, decresce nel secondo e ha un massimo assoluto
nel punto
.
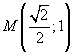La derivata seconda è
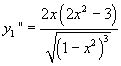
Il denominatore di questa derivata, nei punti interni dell'intervallo considerato, è positivo. Per questi punti il segno della derivata seconda coincide con quello del numeratore che è negativo. Per x=0, la derivata seconda si annulla. Tenendo conto della simmetria, si deduce che la curva di equazione y1 ha un flesso nell'origine, concavità negativa nel primo quadrante e positiva nel terzo. La tangente a γ nell'origine è y=2x.
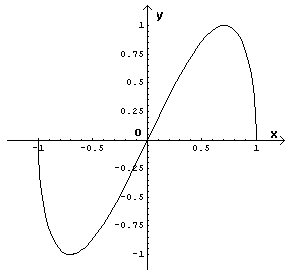
Unendo il grafico di y1 con quello simmetrico di y2, il tracciato completo della curva γ risulta
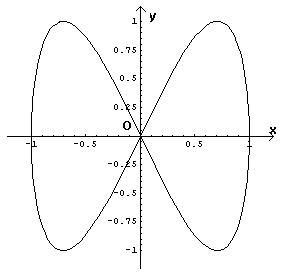
L'area circoscritta da γ è quadrupla di quella delimitata dall'arco di γ nel primo quadrante e dall'asse delle ascisse. Dunque:
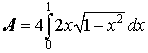
Il calcolo dell'integrale è facilitato dalla sostituzione di variabile
da cui
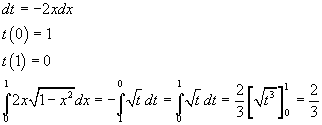
L'area richiesta misura
Il volume indicato è doppio di quello generato dalla rotazione dall'arco di γ nel primo quadrante:
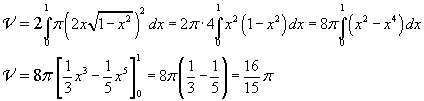
La coordinata polare ρ in funzione delle coordinate cartesiane x e
y è 
.
Dunque
