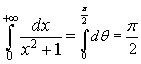Quesiti

testo della prova

Quesito 1

Disegnando nello stesso piano cartesiano Oxy le funzioni a primo e secondo membro dell'equazione si ha

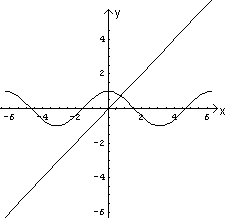
Le due curve si intersecano in un punto di ascissa compresa tra 0 e π/2 che può essere interpretata come soluzione dell'equazione assegnata.

Assumendo 0 come valore x₀ iniziale della successione, dal metodo delle tangenti, che applicato in questo caso dà , si ottiene

• x₁ = 1.000000
• x₂ ≅ 0.750364
• x₃ ≅ 0.739113
• x₄ ≅ 0.739085

Quesito 2

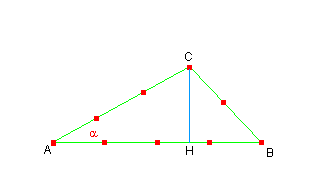
cos α può essere ricavato con il teorema del coseno:

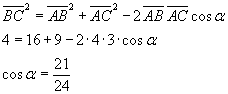
e quindi

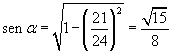
La misura di CH, altezza relativa al lato AB, è dunque

Il volume della figura che si ottiene ruotando il triangolo attorno al lato AB è la somma dei volumi di due coni entrambi con raggio di base CH e altezze rispettivamente AH e HB.

Quesito 3

Rappresentando (non in scala) i punti di osservazione con A e B, con α e β gli angoli corrispondenti, con S la cima del vulcano e con H la sua proiezione sull'orizzontale, si ha

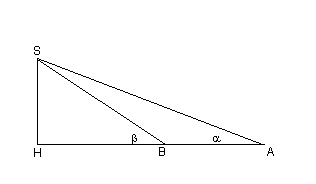
Applicando il teorema dei seni al triangolo ABS si ha

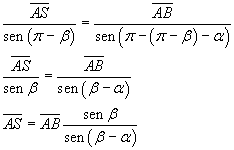
Nel triangolo AHS si ha

In definitiva

Quesito 4

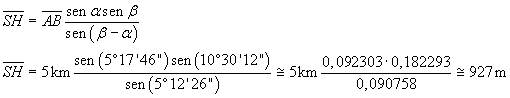
L'esponenziale naturale e^x è reale per ogni x reale e tale risulta anche la funzione cosh x, in quanto esprimibile come combinazione lineare di due esponenziali. Inoltre cosh -x = cosh x: dunque cosh x è pari, ha un minimo assoluto per x = 0 e diverge positivamente per x → ∞. Il suo codominio è [1; ∞[. Questo intervallo è il dominio della funzione inversa che, data la parità della funzione diretta, non è univoca. Perché cosh x sia invertibile bisogna che anche la funzione inversa sia univoca: ciò si può ottenere restringendo dominio di cosh x a [0; ∞[.

Con questa restrizione l'espressione della funzione inversa, detta arcocoseno iperbolico, si ottiene da esprimendo x in funzione di y.

L'ultima uguaglianza ottenuta manifesta che:

• x = arccosh y non è univoca;
• l'argomento y di questa funzione deve essere ≥ 1.

Perché la funzione inversa risulti univoca e produca valori non negativi, bisogna che, nell'ultima uguaglianza, l'argomento del logaritmo, per y ≥ 1, sia ≥ 1, cosa impossibile se si ammette il segno di sottrazione. Dunque:

Quesito 5

Dallo sviluppo in serie di Maclaurin dell'arcotangente circolare

si ottiene la nota serie di Leibniz

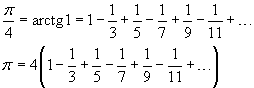
Per rendere più efficiente il calcolo della somma tra parentesi conviene sommare due a due i suoi termini:

Una funzione Javascript che approssimi il valore di π calcolando la somma di un numero n prefissato di addendi può essere la seguente.

function calcoloPi(nc)
{
  nc = parseInt(nc);
  var valore=0;
  var i=0, j=1, denominatore=0;
  for (i=0; i<nc; i++)
    {
      denominatore = j*(j+2);
      valore += 1/denominatore;
      j += 4;
    }
  return 8*valore; 
}

Ma come si può sperimentare nella form riportata, gli algoritmi basati sulla serie di Leibniz convergono troppo lentamente. Sono stati proposti molti metodi più veloci, come, ad esempio, quello di Bailey, Borwein, Plouffe, basato sull'identità

che, in Javascript, può essere implementato dalla seguente funzione:

function calcoloPiBBP(ni)
{
  ni = parseInt(ni);
  var i, j, termine, pot16=1, valorePi = 0;
  for (i=0; i<ni; i++)
    {
      j = i*8+1;
      termine = 4/j;
      j += 3;
      termine -= 2/j;
      j++;
      termine -= 1/j;
      j++;
      termine -= 1/j;
      termine /= pot16;
      valorePi += termine;
      pot16 *= 16;
    }
  return valorePi;
}

Quesito 6

Il vettore di posizione s è l'integrale rispetto al tempo del vettore di velocità v. Dunque

Dalle condizioni iniziali si ha

L'equazione oraria del moto è quindi

da cui

Quesito 7

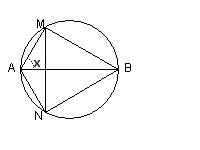
La piramide indicata ha altezza costante a, dunque il suo volume è direttamente proporzionale alla superficie della base AMN che è un triangolo isoscele di lati AM e AN e base MN. L'area di questo triangolo risulta

  con .

Analizzando il segno della derivata prima dell'area si ha

Nell'intervallo considerato il quadrato del coseno è positivo, dunque basta considerare

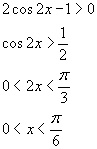
L'area del triangolo e il volume della piramide hanno un massimo per e il volume massimo della piramide risulta

Quesito 8

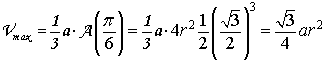
Perché la funzione proposta risulta continua per x=0 è necessario che

Perché la funzione sia derivabile per x=0 è necessario che per questo argomento le derivate sinistra e destra coincidano. La derivata sinistra è , la derivata destra è , quindi .

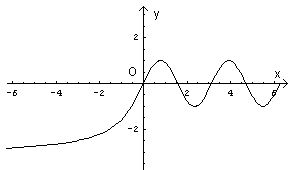
In definitiva si ottiene che l'espressione della funzione a sinistra di 0 è

e il diagramma della funzione in [-2π ; 2π] è

Quesito 9

La funzione integranda è rappresentata nel piano cartesiano Oxy da una gaussiana con flesso in . Nell'intervallo di integrazione assegnato la concavità è negativa in [0;x_F[ e positiva in ]x_F;1]. Applicando il metodo dei trapezi si ha un'approssimazione per difetto nel primo intervallo e per eccesso nel secondo; le approssimazioni si compensano almeno parzialmente.

Suddividendo l'intervallo di integrazione in segmenti di ampiezza 1/5, un'approssimazione dell'integrale è data da

Quesito 10

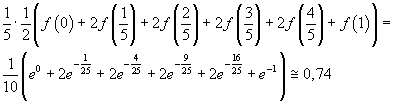
La funzione proposta è pari e definita positiva su tutto l'insieme dei reali. L'area compresa dalla curva da essa rappresentata nel piano cartesiano a l'asse della ascisse è data dall'integral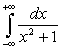e . Data la simmetria della funzione, conviene calcolare 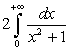. Si ha

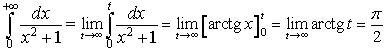
L'area in questione vale dunque π e coincide con quella di una circonferenza di raggio 1.

Si può pervenire allo stesso risultato con la sostituzione di variabile

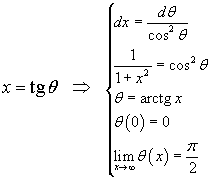
da cui si ha