Sia f(x) una funzione reale di variabile reale tale che valgano le seguenti condizioni
f (xo )>0, f' (xo )>0, f'' (xo )=0,
dove xo è un particolare valore reale.
Spiegare perché tali condizioni non sono sufficienti a determinare l'andamento di f(x) in un intorno di xo.
Trovare almeno tre funzioni polinomiali f(x) di grado superiore al 1°, aventi andamenti diversi in xo=0, tali che
f(0)=1, f'(0)=1, f''(0)=0.
Determinare, se possibile, tutte le retta tangenti ai grafici delle funzioni trovate e parallele alla retta di equazione
y = x + 1.A complemento del problema dimostrare la formula che esprime la derivata, rispetto a x,
della funzione xn dove n è un intero qualsiasi non nullo.
Nel piano, riferito ad un sistema monometrico di assi cartesiani ortogonali (Oxy),
sono assegnati i punti
A(0,2), B(1,1), C(1,0).
-
Trovare l'equazione della circonferenza γ inscritta nel triangolo OAB.
Determinare le equazioni dell'affinità α che ha come punti uniti i punti O e C e trasforma il punto B nel punto A.
Calcolare l'area del triangolo CAA', dove A' è il punto trasformato di A nell'affinità α.
Stabilire se l'affinità &alpha ha altri punti uniti, oltre ad O e C, e trovare le sue rette unite.
Stabilire quali, fra le rette unite trovate, risultano tangenti o esterne a γ.
Assegnata la funzione
![]()
dove il logaritmo si intende in base e, il candidato:
determini per quali valori di a e b la f(x) ha un minimo relativo nel punto
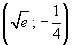
disegni la curva grafico della f(x) per i valori di a e b così ottenuti e calcoli l'area della regione finita da essa delimitata con l'asse x.
Calcoli infine la probabilità che lanciando un dado cinque volte, esca per tre volte lo stesso numero.
Risoluzione