Problema 1

Quesito 1

La prima equazione, che può essere scritta

rappresenta una retta parallela alla bisettrice del II e IV quadrante (in seguito indicata con β )con intercetta a

La seconda equazione, che può essere scritta

rappresenta una retta passante per l'origine di coefficiente angolare 1/a.

Se a>0 si ha un grafico del seguente tipo

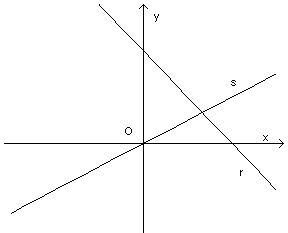
che evidenzia l'esistenza di una soluzione con x e y entrambe positive.

Se a<0 si ha un grafico del seguente tipo

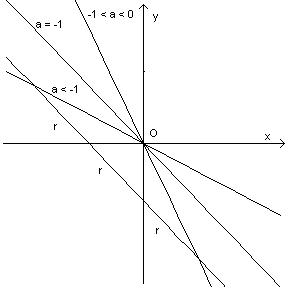
da cui si deduce che per -1<a<0 c'è una soluzione con x positiva e y negativa;
per a=-1 non c'è soluzione;
per -∞<a<-1 c'è una soluzione con x negativa e y positiva.

Una conferma diretta dell'analisi svolta si ha risolvendo il sistema

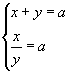
Si ottiene

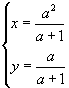
e risulta immediato analizzare i segni di x e y al variare di a.

Quesito 2

L'equazione del luogo γ si ottiene immediatamente dal sistema

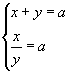
eliminando il parametro a

Si ottiene

Va osservato che y non può essere nullo, quindi non lo può essere nemmeno x: l'origine O(0;0) non appartiene al luogo γ.

Quesito 3

Dovendo rappresentare anche la curva γ' simmetrica di γ rispetto a β e ricordando che le equazioni di una simmetria rispetto a tale retta sono

conviene ricavare subito l'equazione di γ', studiare questa funzione, rappresentarla nel piano cartesiano e dedurre dal suo grafico, per simmetria, il grafico di γ.

Si ottiene immediatamente

STUDIO

• x non può essere nulla.
• Il dominio della funzione è D=]-∞ ; 0[ U ]0 ; 1[ U ]1 ; ∞[ .
• La funzione, nel dominio, è positiva per x <1, negativa per x>1 e non si annulla mai.
• Dall'andamento del segno e dai gradi del numeratore e del denominatore si ha
  
• Per x=1 la funzione ha una singolarità:
  
  la singolarità è di seconda specie; il grafico ha un asintoto verticale x=1.
• Per x=0 la funzione ha una singolarità:
  
  la singolarità è eliminabile.
• i limiti
  
  convergono; il grafico ammette l'asintoto obliquo y = -x -1
• la derivata prima è
  
  e, nel dominio, il suo segno dipende solo dal segno del numeratore;
  -risulta positiva in ]0 ; 1[ U ]1 ; 2[ qui la funzione è crescente;
  -risulta negativa in ]-∞ ; 0[ U ]2 ; +∞[: qui la funzione è decrescente;
  -si annulla solo per x=2: qui la funzione ha un massimo relativo di ordinata -4 M(2 ; -4); -la funzione non ha minimi relativi;
• la derivata seconda è
  
  positiva, nel dominio, per x<1 e negativa per x>1; la concavità ha l'andamento del segno di y'' e non ci sono flessi.

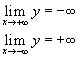
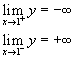
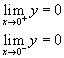
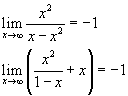
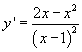
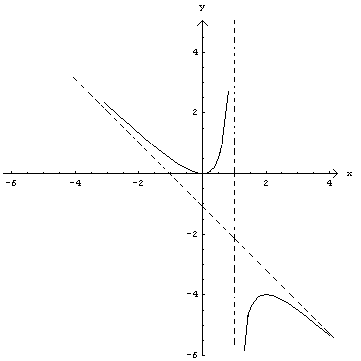
GRAFICO DI γ'

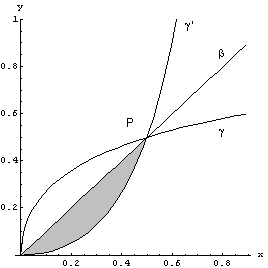
Tracciando i rami simmetrici rispetto a β si ha infine

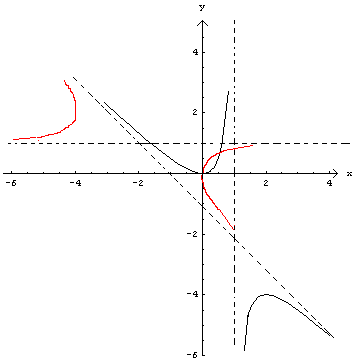
Va ribadito che l'origine O degli assi non appartiene a nessuno dei due grafici.

Quesito 4

Per calcolare l'area richiesta bisogna innanzitutto calcolare l'ascissa del punto comune alle due curve. A questo scopo, data la simmetria, è sufficiente calcolare l'ascissa dell'intersezione tra γ' e la bisettrice β.

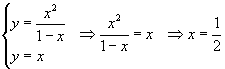
Le due curve si intersecano in

Sempre sfruttando la simmetria, l'area richiesta può essere calcolata raddoppiando l'area delimitata da β e da γ'

Esprimendo la funzione differenza tra β e γ' nel modo più conveniente per l'integrazione

e ricordando che per x=0 c'è una singolarità, l'area richiesta si ottiene nel seguente modo

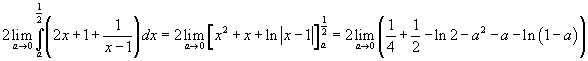
In definitiva si ottiene

Un'approssimazione numerica dell'integrale

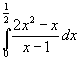
può essere ottenuta con il metodo dei trapezi

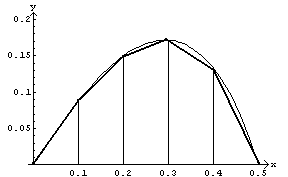
Dividendo l'intervallo di integrazione in cinque parti di ampiezza 0,1 e calcolando i valori della funzione integranda in 0,1; 0,2; 0,3; 0,4; e applicando il metodo si ha

Moltiplicando per 2 si ottiene circa 0,1088.

Quesito 5

Se nell'equazione di γ si pone x=1 si ha

Questa equazione (per 0 < y < 1) è equivalente alla proporzione che definisce φ, il reciproco del numero aureo

Quindi una soluzione di questa equazione è data da y=φ

φ è la sezione aurea dell'unità e compare in molte situazioni matematiche: lato del decagono e del pentagono regolare, funzioni trigonometriche per angoli di 18° e 36°, successioni di Fibonacci, ecc...