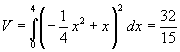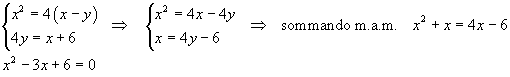
Le curve hanno punti comuni se il sistema delle loro equazioni ha soluzioni.
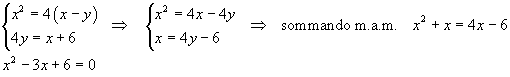
L'equazione risolvente ha discriminante negativo: non ci sono soluzioni reali.
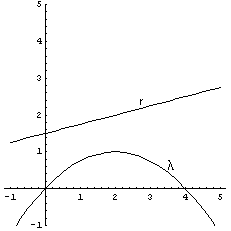
La distanza di un punto
![]() di
λ dalla retta r è data da
di
λ dalla retta r è data da
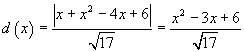
Questa funzione, avendo andamento parabolico, ha il minimo per x=-b/2a, quindi
![]()
La retta s deve aver coefficiente angolare e intercetta opposti a quelli di r: la sua equazione è quindi
![]()
Le intersezioni tra se λ si determinano risolvendo il sistema
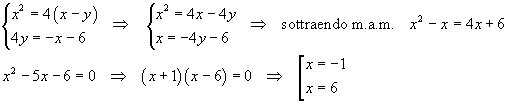
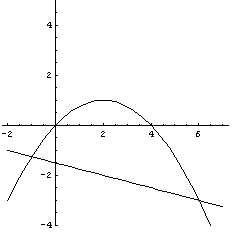
L'area di segmenti parabolici di questo genere, nota l'equazione della parabola e note le ascisse degli estremi A e B del segmento può essere determinata direttamente:
![]()
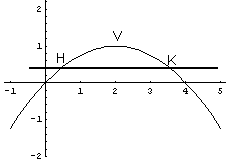
λ interseca l'asse delle ascisse nell'origine e nel punto P di ascissa 4 e ha
vertice in V(2;1). Per il teorema di Archimede
l'area del segmento parabolico retto è proporzionale a quella del rettangolo circoscritto, che ha area 4.
Bisogna allora individuare la retta parallela all'asse delle ascisse che individui due
punti H e K, entrambi di ordinata c compresa tra 0 e 1, tali che il rettangolo
circoscritto al segmento HKV abbia area 2. Le ascisse di H e K sono date dalla soluzione
dell'equazione
![]() .
.
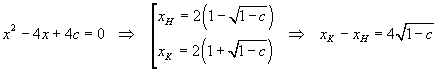
L'altezza del rettangolo è 1-c, quindi deve essere
![]()
Ogni sezione del solido indicato ha superficie
![]()
con x compreso tra 0 e 4. Associando ad ogni superficie uno 'spessore' dx, il volume chiesto si ottiene dall'integrale