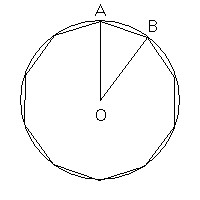

Per ognuno dei lati di un decagono, tracciando i segmenti dagli estremi al centro, si ottiene un triangolo aureo di primo tipo, cioè un triangolo isoscele in cui l'angolo al vertice misura π/5 (36°) e gli angoli alla base misurano il doppio.
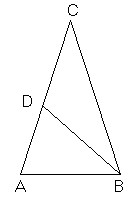
In questi triangoli aurei AC:AB=AB:(AC-AB), cioè la base è la sezione aurea del lato; il rapporto tra base e lato vale quindi
![]()
Detto L10 il lato del decagono inscritto in una circonferenza di raggio r si ha quindi L10=rφ.
Si ha inoltre
![]()
Uguagliando le due espressioni di L10 si ottiene
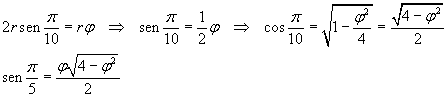
Limitandosi alla considerazione di curve γ nel piano Oxy, di equazione esplicita y=y(x), la retta r di equazione y=mx+q si dice tangente a γ nel suo punto P(xP;yP) se (P∈γ)∧(P∈r)∧(m=y'(xP)).
Tutti i punti di ascissa x tale che senx=1 appartengono oltre che alla curva anche alla retta y=x; in tutti questi punti cosx=0 e la derivata y'=senx+x cosx è uguale al coefficiente angolare della retta; dunque in tutti questi punti si ha tangenza.
Analogamente tutti i punti di ascissa x tale che senx=-1 appartengono sia alla curva sia alla retta y=-x; in tutti questi punti cosx=0 e la derivata y'=senx+x cosx è uguale al coefficiente angolare della retta; dunque in tutti questi punti si ha tangenza.
Se due punti P(x;y) e P'(x';y') sono simmetrici rispetto ad una retta r parallela alla bisettrice b del I° quadrante e di equazione y=x+q, essi possono essere interpretati come i vertici opposti di un quadrato il cui centro C giace su r.
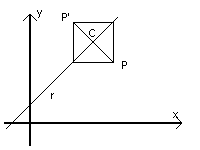
Per l'apparenenza di ![]() a r si ha
a r si ha
![]()
Dall'uguaglianza delle misure dei lati del quadrato si ha inoltre
![]()
Unendo i due risultati
![]()
Le equazioni ottenute corrispondono quindi ad una simmetria rispetto ad una retta parallela a b; in particolare, per q=0, si hanno le equazioni di una simmetria rispetto a b. Indicando con σ quest'ultima simmetria e con φ qualunque altra, applicando ad un punto P(x;y) prima σ, poi φ si ha:
![]()
cioè una traslazione. Quella del testo si ottiene per q=-√5
Applicando ad un punto P(x;y) prima φ, poi σ si ha:
![]()
Usando il sistema c.g.s. il volume della lattina è V=400cm3. Indicando con S la superficie totale si ha
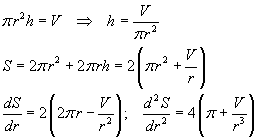
Azzerando la derivata prima si ha
![]()
valore che rende positiva la derivata seconda. Per questo valore la superficie totale ha un minimo
![]()
corrispondente ad un raggio di base r e ad un'altezza h
![]()
Il numero di Nepero e può essere definito in molti modi. Conoscendo le funzioni iperboliche, il più semplice e diretto potrebbe essere
![]()
Può essere definito com il numero reale > 1 tale che l'integrale della funzione f(x)=1/x da 1 a questo numero valga 1.
Dallo sviluppo in serie di MacLaurin dell'esponenziale naturale si ottiene anche
![]()
e può anche essere definito come
![]()
Il numero e è la base della funzione esponenziale e dei logaritmi naturali. Come base di funzioni esponenziali reali o complesse appare in molti problemi di matematica (equazioni differenziali, funzioni d'onda,...). Notissime sono le formule di Eulero per seno e coseno circolari. Appare in quella che da molti è definita "la più bella formula matematica": eiπ+1=0
Un modo per approssimarne a piacere il valore può basarsi sullo sviluppo in serie
![]()
Si sommano i reciproci dei fattoriali fino a che non si ottiene un addendo minore della precisione desiderata, come nella seguente funzione Javascript.
function calcoloNepero(eps)
{
lettura = eps;
eps = Math.abs(parseFloat(eps));
if (isNaN(eps))
{
alert(lettura+": input sbagliato");
return 0;
}
if (eps>0.001)
{
document.nepero.epsilon.value = 0.001;
eps=0.001;
}
ris=1;
i=1;
fatt=1;
rec=1;
while (rec>eps)
{
fatt *=i;
rec = 1/fatt;
ris += rec;
i++;
}
return ris;
}
Le equazioni di una omotetia di rapporto |k| sono in generale
![]()
Applicando questa trasformazione alla retta y=2x+1 si ottiene
![]()
Perché la retta trasformata coincida con la retta y=2x-4 bisogna che k sia uguale a -4.
Definizione ricorsiva: per numeri naturali n non negativi, se (n=0)∨(n=1), n!=1; altrimenti n!=n(n-1)!
n! rappresenta il numero delle permutazioni semplici di n elementi.
Le permutazioni di due elementi a e b con a ripetuto n-k volte e b ripetuto k volte sono
![]()
Queste permutazioni rappresentano il numero delle volte in cui compare il prodotto an-kbk nello sviluppo della potenza n-esima del binomio a+b; coincidono quindi con i coefficienti dello sviluppo di tale potenza e sono detti coefficienti binomiali spesso indicati con
![]()
Ricavando dalla prima equazione l'espressione di et in funzione di x e sostituendo tale espressione nella seconda equazione si ottiene l'espressione di y in funzione di x:
![]()
La derivata di questa funzione è
![]() che per x=3 vale -1. L'equazione della
tangente nel punto indicato è quindi
che per x=3 vale -1. L'equazione della
tangente nel punto indicato è quindi
![]()
10 si può ottenere da (4,6), (5,5), (6,4), cioè in 3 modi su 36 possibili esiti. Dunque la probabilità chiesta è
![]()
La seconda probabilità chiesta si calcola applicando il teorema delle prove ripetute:
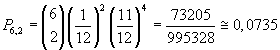
Per calcolare la terza probabilità conviene calcolare la probabilità di 0 esiti su 6 lanci, la probabilità di 1 esito su sei lanci e poi sottrarre da 1 la somma delle due probabilità.
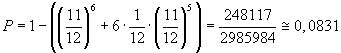
Si. Indicando con y l'età media degli ultrasessantenni e con x l'età media degli infrasessantenni si ha
![]()
Ovviamente x>0, quindi y<75