Questionario - 2009

Quesito 1

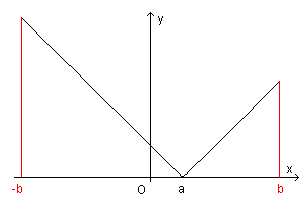
Il grafico della funzione integranda |x-a| ha la seguente forma

L'integrale proposto può essere interpretato geometricamente come la metà della somma delle aree di due quadrati di lati rispettivamente b+a e b-a. Quindi

Quesito 2

• Perché un'applicazione sia biiettiva bisogna che gli insiemi (dominio e codominio) siano equipotenti, ma A e B non lo sono: non possono esistere applicazioni biiettive.
• Perché un'applicazione sia iniettiva bisogna che il la cardinalità del codominio sia superiore a quella del dominio, ma nel caso proposto si verifica il contrario: non possono esistere applicazioni iniettive.
• Possono invece esistere applicazioni suriettive: ad esempio 1→a, 2→a, 3→b, 4→c.

Quesito 3

Perché la moneta non intersechi il bordo di una mattonella bisogna che la distanza del suo centro dal bordo sia minore o al massimo uguale al suo raggio. Detti L la misura del lato della mattonella e D la misura del diametro della moneta, il luogo dei centri è quindi un quadrato di lato L-D. La probabilità chiesta è data dal rapporto tra l'area del quadrato minore e quella del quadrato maggiore.

Quesito 4

Questo quesito è sostanzialmente una replica del quesito 2 dell'esame 2006.

I poliedri regolari (detti solidi platonici) sono solo cinque:

• tetraedro: 4 facce triangolari;
• esaedro (o cubo): 6 facce quadrate;
• ottaedro: 8 facce triangolari;
• dodecaedro: 12 facce pentagonali;
• icosaedro: 20 facce triangolari.

L'affermazione del testo è quindi falsa.

Volendo giustificare il fatto che le facce non possono essere esagoni regolari, si osserva che la somma degli almeno 3 angoli concorrenti nello stesso vertice di un poliedro regolare deve essere minore di 360°, cosa impossibile per gli esagoni regolari in cui angoli interni misurano 120°.

Quesito 5

Nel campo dei numeri reali:

• : è il numero che moltiplicato per 1 dà 0, cioè 0;

• : è un numero che moltiplicato per 0 dà 0, cioè qualsiasi reale: indeterminazione;

• : è un numero che moltiplicato per 0 dà 1: non esiste;

• Per qualunque n ≠ 0: : indeterminazione.

Quesito 6

L'algoritmo di Newton (o delle tangenti), quando applicabile, permette di costruire una successione, di numeri reali convergente ad uno zero di una funzione di variabile reale nel seguente modo

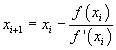
Nel caso proposto si ha quindi

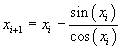
Si ottiene quindi

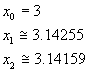
Con due iterazioni si ottiene una buona approssimazione a π che è lo zero della funzione sinx più prossimo a 3.

Quesito 7

Sviluppando in fattoriali il primo membro dell'identità proposta si ha

Operando analogamente sul secondo membro si ottiene

I due termini, nei limiti dei vincoli proposti, sono quindi identici.

Quesito 8

Indicando con u il numero degli uomini e con d il numero delle donne, la somma delle età dei presenti è . La somma delle età degli uomini è e la somma delle età delle donne è . Dunque

Quesito 9

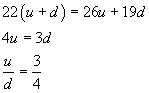
Il principio di Cavalieri afferma che se appoggiando due solidi sullo stesso piano e sezionandoli con piani paralleli al piano di appoggio si ottengono sezioni di area identica, i due solidi hanno ugual volume.

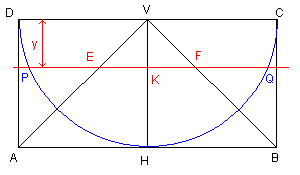
Con riferimento alla figura, detto r il raggio della sfera, sia y (0 < y < r) la distanza del piano di sezione dal vertice del cono. L'area della sezione del cono risulta

L'area della sezione della scodella è data dalla differenza tra l'area del cerchio di raggio r e quella del cerchio di raggio PK. Per il teorema di Pitagora . Dunque

Le sezioni hanno ugual area, dunque i solidi hanno uguale volume.

Quesito 10

La proposizione è uno dei possibili enunciati del cosiddetto quinto postulato di Euclide. Data la non immediata evidenza di tale postulato molti matematici (uno dei più noti fu l'italiano G. G. Saccheri), hanno tentato di dimostrarlo come teorema. L'impossibilità di questa dimostrazione ha indotto diversi matematici del Settecento (tra cui N. I. Lobacevskij e C. F. Gauss) alla conclusione che questo postulato è in linea di principio arbitrario e che può, senza contraddizioni, essere sostituito con postulati alternativi, costruendo geometrie dette non euclidee.