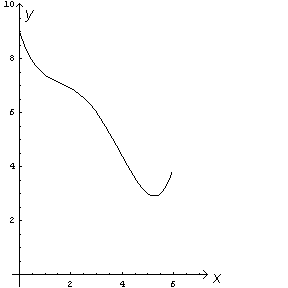
Condizione necessaria e sufficiente perché il grafico della f abbia un flesso per x = xF è che f' si annulli per xF e abbia segni diversi a sinistra e a destra di tale punto. Il grafico proposto mostra che ciò si verifica per x=2 e x=4.
La derivata prima è non positiva, per 0≤x≤5 ed è positiva per 5<x≤6. Dunque f è non crescente nel primo intervallo e crescente nel secondo. Ha quindi un minimo assoluto per x=5.
Da ![]() si ha
si ha
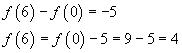
La f non cresce per 0≤x≤5 e non cala per 5<x≤6. Dunque ha il suo massimo assoluto in un estremo dell'intervallo considerato e, confrontando i valori agli estremi, si conclude che il massimo assoluto si ha per x=0 con f(0)=9.
Per x=3, si ha
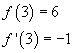
quindi l'equazione della tangente tf al grafico di f in questo punto è
![]()
Inoltre
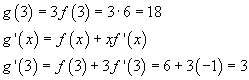
quindi l'equazione della tangente tg al grafico di g in questo punto è
![]()
Detto φ il valore assoluto dell'angolo tra tf e il verso positivo dell'asse delle ascisse
![]()
Detto γ l'angolo tra tg e il verso positivo dell'asse delle ascisse
![]()
L'angolo α tra le due tangenti e dato dalla somma di γ e φ
![]()
Ovviamente due rette che si intersecano di angoli ne formano 4, a due a due opposti al vertice, e quelli non opposti sono supplementari, quindi anche l'angolo supplementare alla somma di γ e φ risponde correttamente al quesito.
![]()