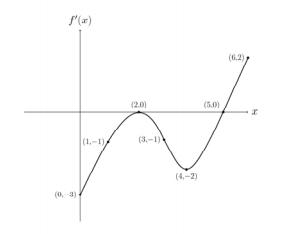
-
Si calcoli 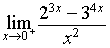
svolgimento
-
Una moneta da 1 euro (il suo diametro è 23,25mm) viene lanciata su un pavimento ricoperto con mattonelle esagonali (regolari)
di lato 10 cm. Quale è la probabilità che la moneta vada a finire internamente a una mattonella (cioè non tagli i lati degli
esagoni)?
svolgimento
-
Sia 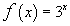 . Per quale valore di x,
approssimato a meno di
. Per quale valore di x,
approssimato a meno di 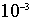 , la pendenza
della retta tangente alla curva nel punto
, la pendenza
della retta tangente alla curva nel punto
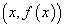 è uguale a 1?
è uguale a 1?
svolgimento
-
L'insieme dei numeri naturali e l'insieme dei numeri razionali sono insiemi equipotenti? Si giustifichi la risposta.
svolgimento
-
Siano dati nello spazio n punti P1, P2, P2,...,Pn. Quanti sono i segmenti che
li congiungono due a due? Quanti i triangoli che hanno per vertici questi punti (supposto che nessuna terna sia allineata)?
Quanti i tetraedri (supposto che nessuna quaterna sia complanare)?
svolgimento
-
Si dimostri che la curva di equazione
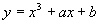 ha un sol punto di flesso rispetto a cui è simmetrica.
ha un sol punto di flesso rispetto a cui è simmetrica.
svolgimento
-
È dato un tetraedro regolare di spigolo l e altezza h. Si determini l'ampiezza dell'angolo α
formato da l e da h.
svolgimento
-
Un'azienda industriale possiede tre stabilimenti (A, B e C). Nello stabilimento A si produce la metà dei pezzi, e di questi
il 10% sono difettosi. Nello stabilimento B si produce un terzo dei pezzi, e il 7% sono difettosi. Nello stabilimento C
si producono i pezzi rimanenti, e il 5% sono difettosi. Sapendo che un pezzo è difettoso, con quale probabilità esso
proviene dallo stabilimento A?
svolgimento
-
Il problema di Erone (matematico alessandrino vissuto probabilmente nella seconda metà del I secolo d.C.) consiste,
assegnati nel piano due punti A e B, situati dalla stessa parte rispetto ad una retta r, nel determinare il cammino
minimo che congiunge A e B toccando r. Si risolva il problema nel modo che si preferisce.
svolgimento
-
Si provi che fra tutti i coni circolari retti circoscritti ad una sfera di raggio r, quello di minima area
laterale ha il vertice che dista
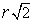 dalla superficie della sfera.
dalla superficie della sfera.
svolgimento
Durata massima della prova: 6 ore.
È consentito soltanto l’uso della calcolatrice non programmabile.
Non è consentito lasciare l’Istituto prima che siano trascorse 3 ore dalla
dettatura del tema.
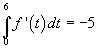 per quale valore di x la funzione f presenta il suo massimo assoluto?
per quale valore di x la funzione f presenta il suo massimo assoluto?