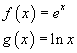
Funzioni
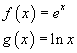
I grafici dell'esponenziale naturale e del logaritmo naturale sono ben noti e non si ritiene necessario procedere ad uno studio analitico delle loro proprietà. Si osserva che, dato che le due funzioni sono l'una l'inversa dell'altra, i loro grafici sono simmetrici rispetto alla bisettrice del I° e III° quadrante.
La regione R di cui va calcolata l'area è rappresentata in azzurro nella figura seguente
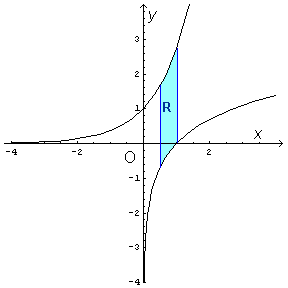
L'area si ottiene dall'integrale
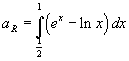
L'integrale indefinito dell'esponenziale è l'esponenziale stessa; l'integrale indefinito del logaritmo è uno tra i più noti di quelli che si calcolano per parti ed è
![]()
Quindi
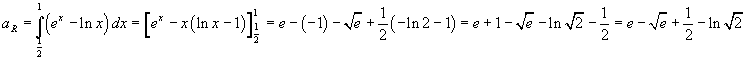
Il solido generato dalla rotazione di R attorno all'asse delle x è determinato solamente dall'arco di esponenziale. Si ha quindi
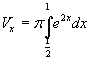
Per calcolare i volume del solido generato dalla rotazione di R attorno all'asse y, conviene suddividere R in tre zone, come mostrato nella seguente figura
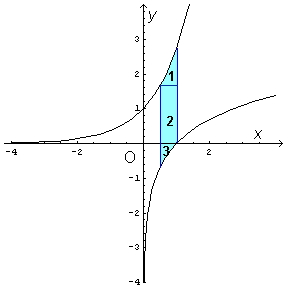
e sommare i volumi generati dalla rotazione delle tre zone.
Il solido generato dalla zona rettangolare 2 può essere calcolato applicando il teorema di Guldin, cioè moltiplicando l'area del rettangolo per la lunghezza della circonferenza percorsa dal suo baricentro:
![]()
Il volume generato dalla rotazione della zona 1 si ottiene sottraendo dal volume di un cilindro di raggio di base 1 e altezza (e-√e) quello generato dalla rotazione di un arco di logaritmica da √e a e:
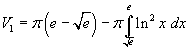
Il volume generato dalla rotazione della zona 3 si ottiene sottraendo dal volume generato dalla rotazione di un arco di esponenziale da -ln2 a 0 il volume di un cilindro di raggio di base 1/2 e altezza ln2:
![]()
Più agilmente, si può concepire il solido T come generato dalla somma di strati cilindrici di spessore infinitesimale dx, di raggio x e altezza ex-ln x. Si ottiene
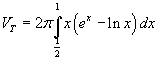
Perché le due tangenti siano parallele, devono essere uguali il loro coefficienti angolari dati dalle loro derivate. Deve cioè essere
![]()
ex è una funzione sempre positiva e crescente, mentre 1/x, negativa per x<0 e positiva per x>0, è una funzione sempre decrescente. Le due funzioni possono uguagliarsi solo per una x positiva, come si può evidenziare graficandole insieme:
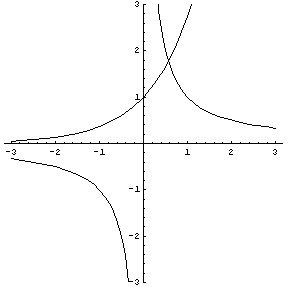
Il grafico mostra che la soluzione è compresa tra 0 e 1. Per approssimare il valore della soluzione si può utilizzare il metodo delle tangenti per la ricerca di uno zero della funzione, iniziando la successione da 1
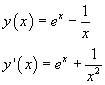
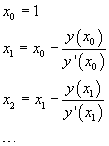
Si ottiene
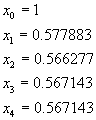
Arrotondato al centesimo, il valore x0 richiesto è
![]()
La derivata della funzione h(x) è data dalla funzione y(x) del quesito precedente, di cui si è visto che si annulla solo una volta per x0≈0.57.
Dal grafico si desume che y(x) è negativa per valori valori minori di x0 e positiva per valori maggiori. Dunque h(x) è decrescente per per x=x0 e crescente per valori maggiori. Quindi per x=x0 si ha un minimo assoluto. Il massimo assoluto va cercato in uno degli estremi.
Si ha
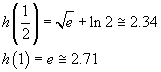
Il massimo assoluto si ha per x=1.