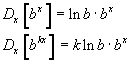
Il limite si calcola applicando il teorema di De l'Hôpital e, ovviamente, derivando appropriatamente le funzioni esponenziali a numeratore. In generale
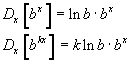
dunque
Il numeratore converge a 
mentre il denominatore
converge a 0 da valori positivi. Dunque
Detto l il lato della piastrella, l'area della piastrella è 6 volte l'area del triangolo equilatero di lato l
Detto d il diametro della moneta, la moneta non taglia il perimetro della piastrella se cade in un esagono concentrico con la piastrella e con lati paralleli a quelli della piastrella. L'area di questo esagono è 6 volte quella di un triangolo equilatero di lato
quindi
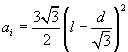
La probabilità richiesta è data dal rapporto tra quest'area e quella della piastrella:
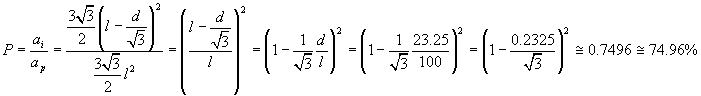
La pendenza, cioè il coefficiente angolare, della tangente ad una curva di equazione f(x) in un punto di ascissa x è data dalla derivata prima dell'equazione. Quindi
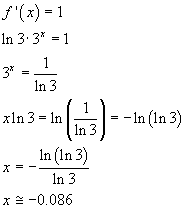
Due insiemi sono equipotenti se è possibile stabilire una corrispondenza biunivoca tra i loro elementi.
Indicando rispettivamente con N, Z e Q gli insiemi dei naturali, degli interi relativi e dei razionali, l'insieme Z è equipotente a N, perché, ad esempio, si può stabilire una corrispondenza biunivoca tra i numeri naturali dispari e gli interi positivi e tra i numeri naturali pari e gli interi negativi.
Un insieme equipotente a N è detto numerabile, quindi Z è numerabile.
In generale, se un insieme S è numerabile, anche il prodotto cartesiano SxS, cioè l'insieme delle coppie ordinate dei suoi elementi, è numerabile. Quindi anche ZxZ è numerabile.
In ZxZ, cioè nell'insieme delle coppie di interi relativi, si può stabilire una relazione di equivalenza, considerando equivalenti due coppie se il prodotto del primo elemento della prima coppia per il secondo elemento della seconda coppia è uguale al prodotto degli altri due rimanenti elementi. Q è definito come l'insieme di queste classi di equivalenza. Ogni elemento di Q, può essere rappresentata da una frazione ridotta ai minimi termini. Q è un sottinsieme infinito di un insieme numerabile, dunque anche Q è numerabile, cioè equipotente ad N.
Il numero dei segmenti è dato dalle combinazioni semplici degli n punti a gruppi di due. Si tratta di combinazioni e non di disposizioni in quanto un segmento, in senso geometrico cioè non orientato, è definito dalla coppia di estremi e non dal loro ordine. Quindi
In modo analogo, per gli altri due quesiti si ha
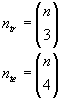
Calcolando le derivate prima e seconda si ha
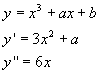
La derivata seconda si annulla per x=0, quindi il suo grafico ha un flesso nel punto F(0,b). Assumendo un sistema di riferimento cartesiano con origine in F, asse y coincidente con quello originario e asse x parallelo a quello del sistema originario, l'equazione della curva diventa
Questa funzione è dispari, quindi la curva è simmetrica rispetto all'origine, cioè rispetto a F.
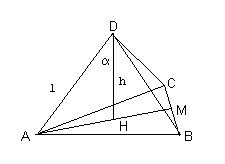
Con riferimento alla figura, il segmento AM è lungo 
;
il segmento AH è 2/3 di AM: 
. Il seno di α
è
.
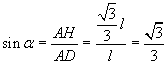Quindi
Il problema può essere risolto applicando meccanicamente il teorema di Bayes, ma può essere trattato in modo più elementare ed intuitivo. Infatti ipotizzando uguale a 600 il numero di pezzi totalmente prodotti in un determinato periodo di tempo:
Il totale di pezzi difettosi è dunque 30+14+5=49 di cui 30 provenienti da A. Quindi la probabilità che un pezzo difettoso provenga da A è
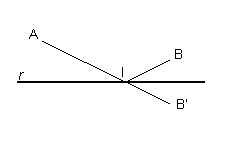
Con riferimento alla figura, dati i punti A e B, sia B' il punto simmetrico di B rispetto alla r. Ovviamente il tracciato più corto tra A e B' è il segmento AB'. Detto I il punto in cui il segmento AB' interseca r, la misura di AB' è uguale alla somme delle misure dei segmenti AI più IB, quindi il cammino AIB è il minimo tra tutti quelli possibili.
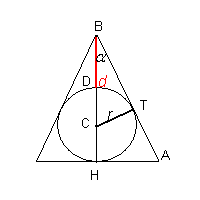
Nella figura si rappresenta una sezione piana della costruzione. Detta d (d>0) la misura del segmento BD, nel triangolo rettangolo BCT si ha
e nel triangolo rettangolo ABH
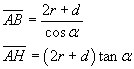
L'area della superficie laterale del cono circoscritto è
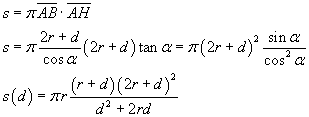
Le derivate di s rispetto a d sono
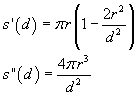
La derivata prima si annulla per
La derivata seconda è comunque positiva, quindi lo zero della derivata prima è un punto di minimo.