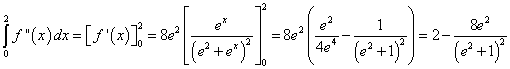. Per la retta di questo
fascio passante per l'origine si ha 
, quindi le coordinate
del massimo di f'(x) sono (2;2).La derivata seconda f''(x) si annulla per x=2, è positiva in un intorno sinistro e negativa in un intorno destro: dunque f'(2) è un massimo relativo di f'(x). f'(2) coincide con il coefficiente angolare della tangente a Γ nel suo punto di ascissa 2.
L'equazione del fascio di rette per F(2;4) è . Per la retta di questo
fascio passante per l'origine si ha , quindi le coordinate
del massimo di f'(x) sono (2;2).
Nell'intervallo ]2,∞[, f'(x) è sempre decrescente, ma sempre maggiore di 0 e ha un flesso dove Λ ha un minimo.
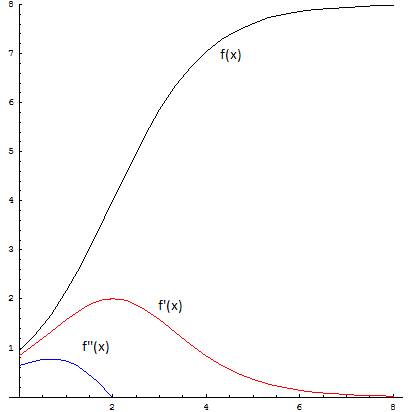
Interpretando x come variabile temporale, la popolazione, a partire dal valore iniziale, è sempre crescente. Il ritmo di crescita aumenta fino al punto di flesso per poi diminuire tendendo a 0 e la popolazione tende a stabilizzarsi.
Il punto F(2;4) appartiene a Γ, dunque 
La derivata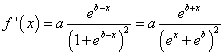 
ha massimo in M(2;2), dunque
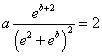
I valori di a e b si ottengono risolvendo il sistema
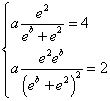
Dividendo membro a membro la seconda equazione per la prima si ha
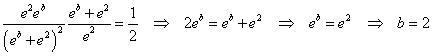
Quindi sostituendo b con 2 nella prima equazione
L'area richiesta è data dall'integrale
