Ministero dell'Istruzione, dell'Università e della Ricerca
ESAME DI STATO DI LICEO SCIENTIFICO
CORSO SPERIMENTALE
Indirizzo: PIANO NAZIONALE INFORMATICA

Tema di MATEMATICA

Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario.

PROBLEMA 1

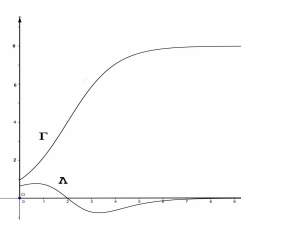
Una funzione f(x) è definita e derivabile, insieme alle sue derivate prima e seconda, in [0,+∞[ e nella figura sono disegnati i grafici Γ e Λ di f(x) e della sua derivata seconda f''(x). La tangente a Γ nel suo punto di flesso, di coordinate (2;4), passa per (0;0), mentre le rette y=8 e y=0 sono asintoti orizzontali per Γ e Λ, rispettivamente. Si dimostri che la funzione f'(x), ovvero la derivata prima di f(x), ha un massimo e se ne determinino le coordinate. Sapendo che per ogni x del dominio è: f''(x) ≤ f'(x) ≤ f(x), qual è un possibile andamento di f'(x)? Si supponga che f(x) costituisca, ovviamente in opportune unità di misura, il modello di crescita di un certo tipo di popolazione. Quali informazioni sulla sua evoluzione si possono dedurre dai grafici in figura e in particolare dal fatto che Γ presenta un asintoto orizzontale e un punto di flesso? Se Γ è il grafico della funzione 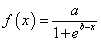, si provi che a = 8 e b = 2. Nell'ipotesi del punto 3), si calcoli l'area della regione di piano delimitata da Λ e dall'asse x sull'intervallo [0,2].

svolgimento

PROBLEMA 2

Sia f la funzione definita per tutti gli x positivi da .

1. Si studi f e si tracci il suo grafico γ su un piano riferito ad un sistema di assi cartesiani ortogonali e monometrici Oxy; accertato che γ presenta sia un punto di flesso che un punto di minimo se ne calcolino, con l'aiuto di una calcolatrice, le ascisse arrotondate alla terza cifra decimale.
2. Sia P il punto in cui γ interseca l'asse x. Si trovi l'equazione della parabola, con asse parallelo all'asse y , passante per l'origine e tangente a γ in P.
3. Sia R la regione delimitata da γ e dall'asse x sull'intervallo aperto a sinistra ]0,1]. Si calcoli l'area di R, illustrando il ragionamento seguito, e la si esprima in mm² avendo supposto l'unità di misura lineare pari a 1 decimetro.
4. Si disegni la curva simmetrica di γ rispetto all'asse y e se ne scriva altresì l'equazione. Similmente si faccia per la curva simmetrica di γ rispetto alla retta y = -1.

svolgimento

QUESTIONARIO

1. Un triangolo ha area 3 e due lati che misurano 2 e 3. Qual è la misura del terzo lato? Si giustifichi la risposta.

   svolgimento

2. Se la funzione ha derivata 5 in x = 1 e derivata 7 in x = 2, qual è la derivata di in x = 1?

   svolgimento

3. Si considerino, nel piano cartesiano, i punti A(2;-1) e B (-6;-8). Si determini l'equazione della retta passante per B e avente distanza massima da A

   svolgimento

4. Di un tronco di piramide retta a base quadrata si conoscono l'altezza h e i lati a e b delle due basi. Si esprima il volume V del tronco in funzione di a, b e h, illustrando il ragionamento seguito.

   svolgimento

5. In un libro si legge: "se per la dilatazione corrispondente a un certo aumento della temperatura un corpo si allunga (in tutte le direzioni) di una certa percentuale (p.es. 0,38%), esso si accresce in volume in proporzione tripla (cioè dell'1,14%), mentre la sua superficie si accresce in proporzione doppia (cioè di 0,76%)". È così? Si motivi esaurientemente la risposta

   svolgimento

6. Con le cifre da 1 a 7 è possibile formare 7!=5040 numeri corrispondenti alle permutazioni delle 7 cifre. Ad esempio i numeri 1234567 e 3546712 corrispondono a due di queste permutazioni. Se i 5040 numeri ottenuti dalle permutazioni si dispongono in ordine crescente qual è il numero che occupa la 5036-esima posizione e quale quello che occupa la 1441-esima posizione?

   svolgimento

7. In un gruppo di 10 persone il 60% ha occhi azzurri. Dal gruppo si selezionano a caso due persone. Quale è la probabilità che nessuna di esse abbia occhi azzurri?

   svolgimento

8. Si mostri, senza utilizzare il teorema di l'Hôpital, che:

   

   svolgimento

9. Tre amici discutono animatamente di numeri reali. Anna afferma che sia i numeri razionali che gli irrazionali sono infiniti e dunque i razionali sono tanti quanti gli irrazionali. Paolo sostiene che gli irrazionali costituiscono dei casi eccezionali, ovvero che la maggior parte dei numeri reali sono razionali. Luisa afferma, invece, il contrario: sia i numeri razionali che gli irrazionali sono infiniti, ma esistono più numeri irrazionali che razionali. Chi ha ragione? Si motivi esaurientemente la risposta.

   svolgimento

10. Si stabilisca per quali valori k∈R l'equazione ammette due soluzioni distinte appartenenti all'intervallo [0,3]. Posto k=3, si approssimi con due cifre decimali la maggiore di tali soluzioni, applicando uno dei metodi iterativi studiati.

    svolgimento

_______________________________________________________________

Durata massima della prova: 6 ore.
È consentito soltanto l’uso della calcolatrice non programmabile.
Non è consentito lasciare l’Istituto prima che siano trascorse 3 ore dalla dettatura del tema.