L'area di un triangolo è data dalla metà del prodotto tra le misure di due lati consecutivi per il seno dell'angolo tra di essi. Nel caso proposto il
seno è 1, quindi l'angolo è retto e i due lati sono i cateti di un triangolo rettangolo di cui il terzo lato è l'ipotenusa. Per il teorema di Pitagora la
sua misura è ![]() .
.
Posto ![]() , si ha
, si ha
![]() . Dai dati si ottiene
. Dai dati si ottiene
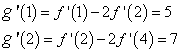
Moltiplicando per 2 i membri della seconda uguaglianza
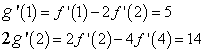
Sommando membro a membro si ha
![]()
cioè il valore della derivata di h(x) per x=1.
La retta per B con massima distanza da A è la perpendicolare per B alla retta AB.
La retta AB ha coefficiente angolare ![]() , quindi l'equazione chiesta è
, quindi l'equazione chiesta è
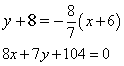
Si supponga di sovrappore al tronco di piramide una piramide retta di base concidente con la base minore del tronco in modo da completare la piramide retta di base quadrata di lato a. L'altezza k di questa seconda piramide è tale che
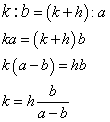
L'altezza della piramide con lato di base a è
![]()
Il volume del tronco di piramide è dato dalla differenza tra i volumi delle due piramidi introdotte:
![]()
Considerando per semplicità un cubo inizialmente di spigolo unitario e quindi di volume unitario e facce di superficie unitaria, dopo la dilatazione il volume è 1.00383 unità cubiche, cioè circa 1.01144337 unità cubiche, con un aumento di circa 1,144337%, mentre la superficie di una faccia è 1.00382 unità quadrate, cioè circa 1.00761444 unità quadrate, con un aumento del 0,761444%.
In generale, il coefficiente di dilatazione volumica è circa il triplo del coefficiente di dilatazione lineare, mentre il coefficiente di dilatazione superficiale è circa il doppio.
Il massimo numero rappresentabile con le sette cifre, cioè quello in posizione 5040, è ovviamente 7654321. Si possono facilmente dedurre i precedenti fino lalla posizione 5036 permutando le ultime cifre in modo da ottenere numeri decrescenti.
| # | numero |
|---|---|
| 5040 | 7654321 |
| 5039 | 7654312 |
| 5038 | 7654231 |
| 5037 | 7654213 |
| 5036 | 7654132 |
Per rispondere al secondo quesito, si osserva che il blocco dei numeri più piccoli della serie è formato da quelli che cominciano per 1 con le rimanenti 6 cifre date dalle permutazioni dei numeri 2-3-4-5-6-7 che sono 6!=720. Il secondo blocco è formato da quelli che cominciano per 2 con le rimanenti cifre date dalle permutazioni dei numeri 1-3-4-5-6-7 che sono pure 720. In totale i numeri che cominciano per 1 o per 2 sono 1440. Dunque il numero successivo, il 1441-esimo, è il più piccolo numero che comincia per 3, cioè 3124567.
Nel gruppo ci sono 6 persone con gli occhi azzurri e 4 con gli occhi non azzurri. Segliendo a caso una persona, la probabilità che non abbia gli occhi azzurri
è 4/10. Scegliendo poi a caso una delle rimanenti, la probabilità che non abbia gli occhi azzurri è 3/9 (probabilità condizionata). La probabilità composta
dei due eventi è ![]() .
.
Posto ![]() il limite proposto è equivalente a
il limite proposto è equivalente a
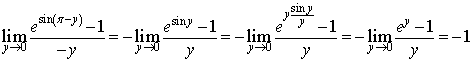
L'insieme dei razionali è equipotente all'insieme dei naturali: è quindi un insieme numerabile con cardinalità ℵ0, mentre l'insieme degli irrazionali ha la potenza del continuo, con cardinalità superiore ad ℵ0.
La funzione a primo membro ![]() rappresenta una cubica
che tocca l'asse x nell'origine e lo interseca per x=3.
rappresenta una cubica
che tocca l'asse x nell'origine e lo interseca per x=3.
La derivata prima ![]() si annulla per x=0 e x=2, valori
per i quali la derivata seconda
si annulla per x=0 e x=2, valori
per i quali la derivata seconda ![]() risulta nel primo caso
positiva e nel secondo caso negativa. Per x=0 si ha il minimo locale O(0;0) e per x=2 il massimo locale M(2;4).
risulta nel primo caso
positiva e nel secondo caso negativa. Per x=0 si ha il minimo locale O(0;0) e per x=2 il massimo locale M(2;4).
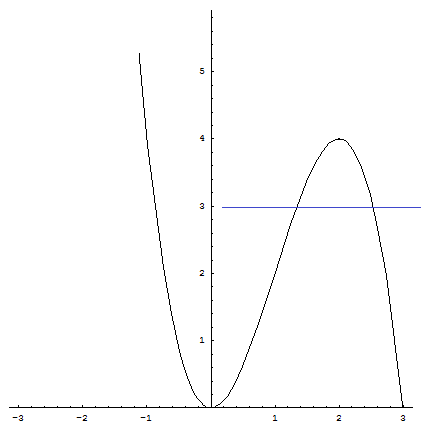
Una retta parallela all'asse delle ascisse interseca la curva in due punti distinti nell'intervallo richiesto solo se ha quota k maggiore di 0 e minore di 4.
In particolare, per k=3, il grafico evidenzia una intersezione di ascissa compresa tra 2.5 e 3. In effetti, la funzione
![]() è tale che F(2.5)=0.125 e F(3)=-2 e, poiché è una
funzione continua, per il teorema di Bolzano, deve avere almeno uno zero in in questo intervallo. Per approssimare a piacere questo zero si può
usale l'algoritmo delle tangenti, assumendo x0=2.5.
è tale che F(2.5)=0.125 e F(3)=-2 e, poiché è una
funzione continua, per il teorema di Bolzano, deve avere almeno uno zero in in questo intervallo. Per approssimare a piacere questo zero si può
usale l'algoritmo delle tangenti, assumendo x0=2.5.
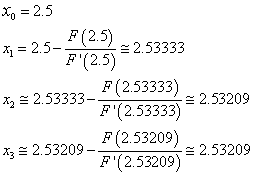
Nell'approssimazione richiesta, lo zero cercato vale circa 2.53.