g(x) è definita solo in un intorno destro di A. In A la tangente geometrica alla semicirconferenza è perpendicolare all'asse delle x, dunque non ha coefficiente angolare e poiché il coefficiente angolare della tangente coincide con il valore della derivata prima, g(x) non ha derivata destra.
g(x) è definita in un intorno completo di O, ma anche in questo caso le tangenti destra e sinistra, pur coincidendo, sono entrambe perpendicolari all'asse x e la funzione non è derivabile. In O c'è un flesso verticale.
g(x) è definita in un intorno completo di B e le tangenti destra e sinistra hanno entrambe coefficiente angolare 0. In B la funzione ha derivata 0.
g(x) è definita in un intorno completo di C. La tangente a sinistra ha coefficiente angolare 0, mentre la tangente a destra ha coefficiente angolare negativo. I coefficienti angolari delle due tangenti non coincidono, dunque la funzione non è derivabile.
g(x) è definita solo in un intorno sinistro di D e la tangente da sinistra è perpendicolare all'asse , dunque, in D, g(x) non ha derivata sinistra.
f(-4) è un integrale definito in cui gli estremi di integrazione sono coincidenti, dunque vale 0.
Il valore assoluto di f(0) è rappresentato geometricamente dall'area della semicirconferenza il cui raggio misura 2, cioè 2π. Dato che la semicirconferenza giace nel semipiano dell y negative, l'integrale vale -2π.
L'integrale da 0 a 2 è rappresentato da un'area metà di quella precedente ed è positivo. Dunque f(2) è dato dalla somma degli integrali da -4 a 0 e da 0 a 2 e vale -π.
L'integrale da 2 a 4 è rappresentato geometricamente dall'area di un quadrato di lato di misura 2, cioè 4. f(4) si ottiene da f(2) aggiungendo 4, quindi f(4)=4-π.
L'integrale da 4 a 6 è rappresentato geometricamente dalla metà di un segmento parabolico retto che, per il teorema di Archimede, vale 2/3 dell'area del rettangolo circoscritto, dunque 8/3. f(6) è quindi uguale a f(4)+8/3, cioè 20/3-π
Per il calcolo di f(1) si nota che l'area sottesa dalla curva tra 0 e 1 si ottiene sottraendo dall'area di 1/6 di circonferenza di raggio 2 l'area di un triangolo di base 1 e altezza √3, cioè
![]()
quindi f(1) si ottiene aggiungendo quest'area a f(0)
![]()
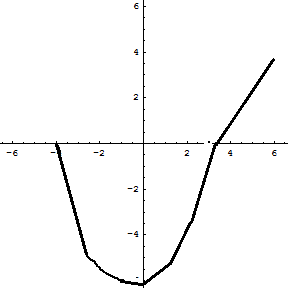
Interpretando geometricamente la f(x), dal valore iniziale 0 assunto per x=-4, essa decresce monotonicamente fino a x=0 dove raggiunge il minimo assoluto -2π, quindi cresce e rimane negativa fino a che l'area sottesa dall'arco di ordinate positive di curva risulta uguale a 4π
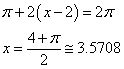
Per questo valore la f(x) è nulla, quindi diventa positiva e continua a crescere fino a raggiungere il massimo assoluto f(6).
La derivata seconda di f(x) è data dalla derivata prima di g(x) il cui andamento è desumibile dall'andamento del coefficiente angolare della tangente al grafico di g(x). Risulta:
La risposta alla prima domanda è già stata data ne quesito 3.
Sempre nel quesito 3 si sono forniti gli elementi per rappresentare l'andamento della f(x).