Funzione:
Con la traslazione 
l'origine
viene spostata nel punto (2;0) e l'equazione della curva è data da
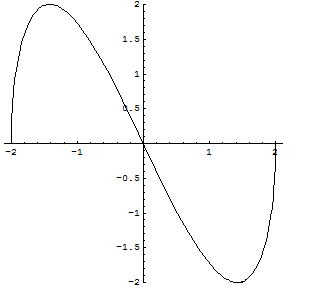
È facile verificare che f(X) è un funzione dispari, dunque simmetrica rispetto all'origine.
Il coefficiente angolare della tangente in un punto di ascissa xP è data dalla derivata in xP. L'equazione della derivata è
Il coefficiente angolare della tangente nell'origine è
L'angolo richiesto è dato dall'arcotangente del coefficiente angolare. Usando una calcolatrice settata sui gradi sessagesimali e usando la funzione dms si ottiene circa -63°26'6".
La risposta al quesito è immediata se si considera l'equazione della curva traslata e i punti di ascisse ±t. Dato che la derivata f'(X) calcolata al punto 1 è una funzione pari, ha lo stesso valore per due punti di ascissa opposta; di conseguenza i coefficienti angolari delle tangenti sono uguali e quindi le tangenti sono parallele.
Sempre riferendosi alla curva traslata di equazione f(X) si osserva che la derivata tende a +∞ per X=±2, si annulla per X=±√2 e raggiunge il minimo -2 per X=0. Dato che tale derivata è una funzione continua, per il teorema di Bolzano, può almeno una volta assumere tutti i valori ≥-2. In particolare può assumere il valore -23/12, corrispondente al coefficiente angolare della seconda retta proposta, ma non può assumere il valore -21/10 corrispondente al coefficiente angolare della prima retta proposta. Esistono quindi tangenti parallele alla seconda retta ma non esistono tangenti parallele alla prima.
Intendendo l'area in senso geometrico, conviene calcolare il valore dell'integrale della funzione traslata da -2 a 0 e poi raddoppiarlo. Si ha
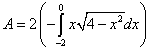
Il calcolo dell'integrale è facilitato dalla sostituzione di variabile
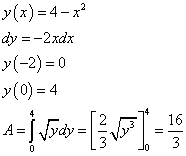
Continuando a lavorare sulla curva traslata di equazione
si ha
La funzione h(X) assume valore 1 quando f(X) è uguale a π/2.
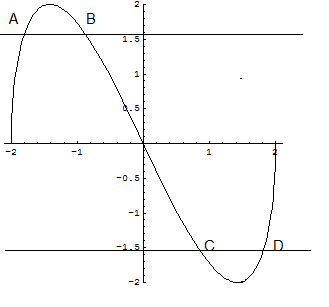
Si verifica graficamente che i punti sono 2, indicati in figura con A e B, per la h(X) e ovviamente anche per la h(x).
Una funzione seno ha massimi assoluti di valore 1 quando il suo argomento è π/2, dunque la h(X) ha massimi assoluti per x = xA e xB. Ovviamente per h(x) queste ascisse vanno aumentate di 2.
Una funzione seno ha minimi assoluti di valore -1 quando il suo argomento è -π/2, dunque la h(X) ha minimi assoluti per x = xC e xD. Ovviamente per h(x) queste ascisse vanno aumentate di 2.
Dato che per per xA e xB si hanno due massimi, per il teorema di Rolle tra
xA e xB ci deve essere un minimo relativo la cui ascissa coincide
con il massimante di f(X). Analogamente tra xC
e xD ci deve essere un massimo relativo la cui ascissa coincide con il minimante di f(X).
I valori massimante e minimante di f(X) si ottengono dall'azzeramento della sua derivata prima
e sono ±√2
con massimo e minimo 2 e -2.
Quindi le equazioni h(X)=k e h(x)=k hanno 4 soluzioni per k compreso tra il massimo assoluto e il minimo relativo o tra il massimo relativo e il minimo assoluto cioè
Data la simmetria, l'integrale richiesto è ovviamente nullo.